- 真题试卷
- 模拟试卷
- 预测试卷
3.在等差数列


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.在正方体


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.若双曲线

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
1.已知


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2.若集合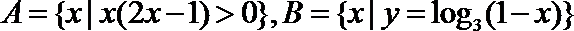
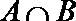
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.若直线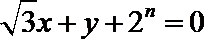
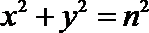
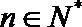
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.已知m,n为两条不重合的直线,
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.若

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.给定性质:
(1)最小正周期
(2)图像关于直线
(3)图像关于点
则下列四个函数中同时具有(1)(2)(3)的是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4. “

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.在




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12. 右表给出一个“三角形数阵”,已知每一列的数成等差数列;从第三行起,每一行的数成等比数列,每一行的公比都相等,记第i行第j列的数为

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18.连续抛掷一枚均匀的骰子(各个面上分别标有数字1,2,3,4,5,6)两次,用(


(1)试问:一共有多少种不同的结果?请列出所有可能的结果;
(2)若

正确答案
(1)共有36种结果
(1,1)(1,2)(1,3)(1,4)(1,5)(1,6)
(2,1)(2,2)(2,3)(2,4)(2,5)(2,6)
(3,1)(3,2)(3,3)(3,4)(3,5)(3,6)
(4,1)(4,2)(4,3)(4,4)(4,5)(4,6)
(5,1)(5,2)(5,3)(5,4)(5,5)(5,6)
(6,1)(6,2)(6,3)(6,4)(6,5)(6,6)
(2)若


记满足
则
故所求事件的概率为
解析
解析已在路上飞奔,马上就到!
知识点
19.如图,四棱锥P-ABCD的底面是边长为2的正方形,侧面PAD是等腰直角三角形,PA=PD,又平面PAD


(1)求侧视图的面积;
(2)求证:平面PDC
(3)求三棱锥E-AFB的体积。
正确答案
(1)


(2)


且平面
又



(3)取AD中点Q,连结PQ.则


且平面


连结CQ并取CQ中点H连结EH,则EH

又
解析
解析已在路上飞奔,马上就到!
知识点
17.已知


(1)求
(2)若

正确答案
(1)
(2)由
则
由

解析
解析已在路上飞奔,马上就到!
知识点
20.已知函数

(1)求
(2)若
正确答案
(1)
由已知得
解得
(2)由已知只须
令





令





在
则
由
解得
解析
解析已在路上飞奔,马上就到!
知识点
21.已知各项均为正数的数列


(1)求数列
(2)若



正确答案
(1)由已知 
当

①-② 得
整理得
又n=1时 


故
(2)由
得
则
=
=

①-②,得
=
解得
解析
解析已在路上飞奔,马上就到!
知识点
22.如图,椭圆

(1)求椭圆C的标准方程;
(2)已知顶点在坐标原点的抛物线的焦点为椭圆的上焦点



(3)若直线


正确答案
答案:
解析
解析已在路上飞奔,马上就到!
知识点
13.命题

正确答案

解析
解析已在路上飞奔,马上就到!
知识点
14.在半径为1的半圆内,放置一个边长为
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15.已知数列


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16. 若曲线
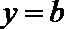
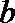
正确答案
[-1,1]
解析
解析已在路上飞奔,马上就到!