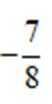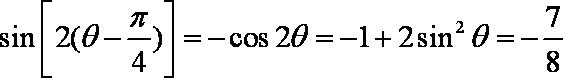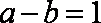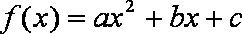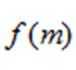- 真题试卷
- 模拟试卷
- 预测试卷
2.设





正确答案
解析
解析:由



知识点
4.已知
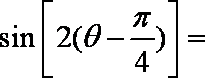
正确答案
解析
解析:
知识点
6.函数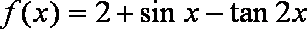
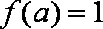
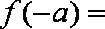
正确答案
3
解析
令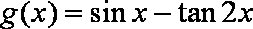
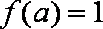
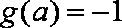
知识点
1.全集



正确答案
解析


知识点
3.函数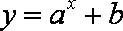
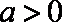
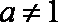
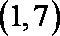
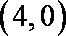
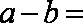
正确答案
1
解析
解析:由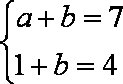
知识点
5.已知圆锥的母线长为
正确答案
解析





知识点
7.设




正确答案
解析
由

知识点
8.关于


正确答案
解析
解析:
知识点
9.若

正确答案
解析

知识点
10.函数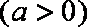
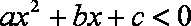
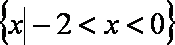
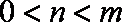
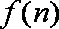

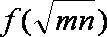
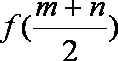
正确答案
解析
由已知得函数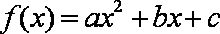
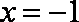
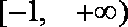
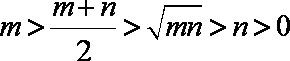
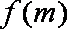
知识点
11.若函数








正确答案
8
解析






知识点
13.若存在


正确答案
解析
函数



知识点
14.如图所示,






正确答案
48
解析
设右焦点为

=
知识点
12.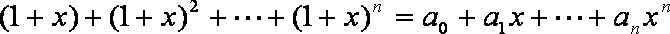
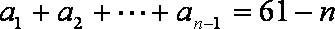
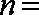
正确答案
5
解析
显然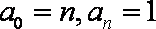
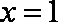
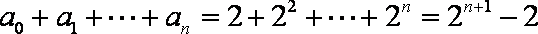
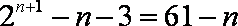
知识点
18.已知数列



(1)



则其中真命题的序号是 ( ).
正确答案
解析
考查数列的通项公式,选C
知识点
17.若复数






正确答案
解析
考查复数的共轭复数的概念,选D
知识点
15.在空间中,下列命题正确的是( ).
正确答案
解析
考查直线,平面的位置关系,选D
知识点
16.设实数




正确答案
解析
考查方程组的解集问题,选B
知识点
19.在长方体






(1) 求几何体

(2)求异面直线

正确答案
见解析。
解析
(1)


左视图如下图所示.
(2)依据题意,有

∴


又
∴
∴异面直线


知识点
20.已知函数


(1)求
(2)当

正确答案
(1)
(2)
解析
(1)设点



于是有
所以,

(2)由(1)可知,
又
所以,
考察正弦函数


于是,
所以,当

知识点
21.有一块铁皮零件,其形状是由边长为











(1)试求出矩形铁皮


(2)试问如何截取(即

正确答案
见解析。
解析
解析:(1)依据题意并结合图形,可知:
1 当点



2 当点




于是,
所以,

(2)由(1)知,当

当


因此,

所以,先在












知识点
22.已知数列



(1)求数列


(2)数列





(3)设


正确答案
(1)
(2)
(3)3
解析
(1) 



∴令

∴数列


∴
(2) 由



故
当

于是,
当

当
又

综上,有
(3)

∴

∴数列



知识点
23.已知点




(1)求曲线
(2)点




(3)已知点





正确答案
见解析。
解析
(1)依据题意,动点

又
因此,动点


所以,所求曲线

(2) 设





=
由





(3)证明:设原点到直线












由
设点
于是,


利用

综合