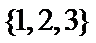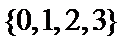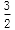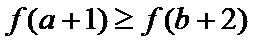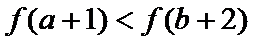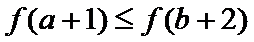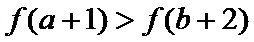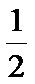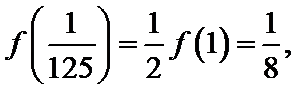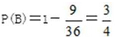- 真题试卷
- 模拟试卷
- 预测试卷
1.若集合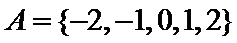
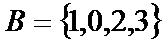
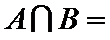
正确答案
解析



而集合


知识点
3.已知命题p: ∀x

正确答案
解析
“





知识点
4.设

正确答案
解析
因为
由零点存在性定理知,


故存在
知识点
7.已知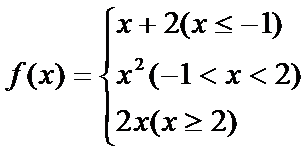
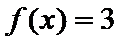
正确答案
解析
若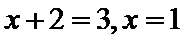
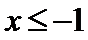
若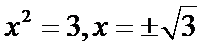
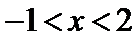
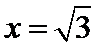
若

综上可知,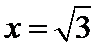
知识点
8.设


正确答案
解析
因为

由给出的图可知对称轴在

所以二次函数的图象为第三个图,图象过原点,
故


知识点
9.偶函数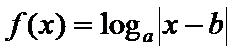
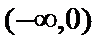
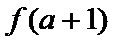
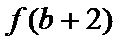
正确答案
解析
因为函数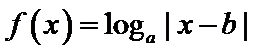
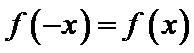
而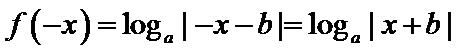
所以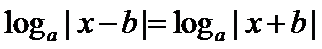
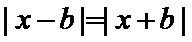
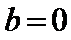
故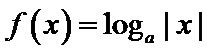
因为当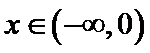
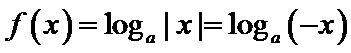
其中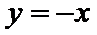
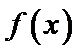
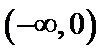
那么,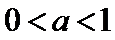
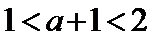
而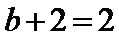
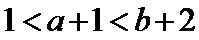
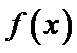
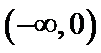
所以在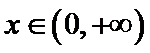
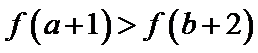
知识点
10.定义在[0,1]上的函数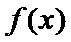
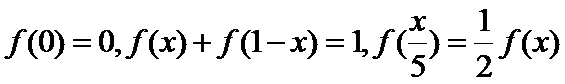
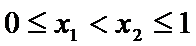
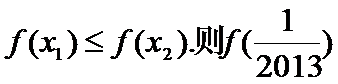
正确答案
解析
由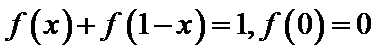
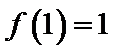
令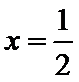
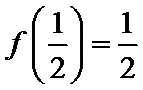
由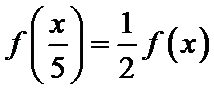
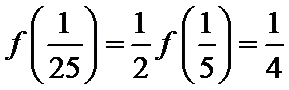
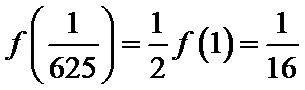
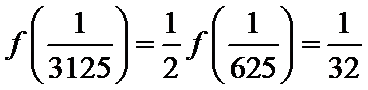
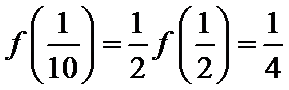
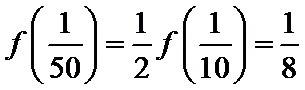
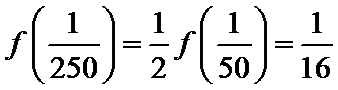
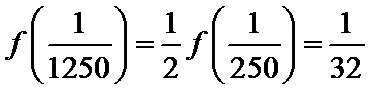
而当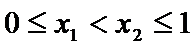
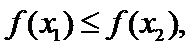
所以当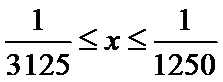
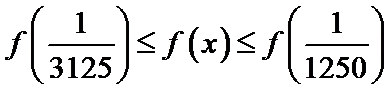
即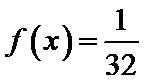
而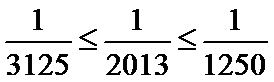
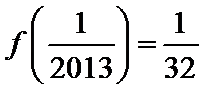
知识点
2.复数
正确答案
解析

知识点
5.设


正确答案
解析
如图,为矩形.
设









两条平行直线,其中一条垂直一个平面,那么另一条也垂直于这个平面,故B正确;
对于C,设









对于D,设









综上可知选B.
知识点
6.设等差数列{an}的前n项和为




正确答案
解析
由





知识点
11.函数
正确答案
解析
要使


知识点
13.设


正确答案
解析
因为
而
故
所以
知识点
12.程序框图(即算法流程图)如图所示,其输出结果是_________
正确答案
31
解析
根据流程线依次执行,

知识点
14.设

正确答案
解析
令
因为

所以单调增区间为
知识点
15.下列几个命题:
①方程

②函数
③设函数



④一条曲线




其中正确的有_______________.
正确答案
①④
解析
方程
则


故
对于②,函数化为
对于③,


对于④,



答案为:①④.
知识点
18.已知函数

(Ⅰ)求函数
(Ⅱ)设











正确答案
解析
解析已在路上飞奔,马上就到!
知识点
20.已知函数
(Ⅰ)若

(Ⅱ)若



(Ⅲ)令



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
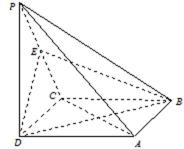
16.如图,在四棱锥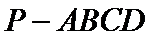
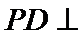
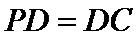
(Ⅰ)证明 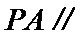
(Ⅱ)求EB与底面ABCD所成的角的正切值.
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17.将一颗骰子先后抛掷2次,观察向上的点数,求:
(Ⅰ)两数之和为5的概率;
(Ⅱ)两数中至少有一个为奇数的概率.
正确答案
将一颗骰子先后抛掷2次,此问题中含有36个等可能基本事件.
(Ⅰ)记“两数之和为5”为事件A,则事件A中含有4个基本事件,所以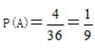
答:两数之和为5的概率为
(Ⅱ)记“两数中至少有一个为奇数”为事件B,则事件B与“两数均为偶数”为对立事件,所以
解析
解析已在路上飞奔,马上就到!
知识点
19.定义在





(Ⅰ)求证:
(Ⅱ)求证:对任意的

(Ⅲ)证明:

正确答案
解析
解析已在路上飞奔,马上就到!