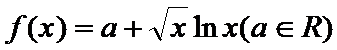- 真题试卷
- 模拟试卷
- 预测试卷
1.已知集合A=

正确答案
解析


考查方向
解题思路
本题考查集合的概念和交集运算,概念的理解能力。解题步骤如下:
读懂题意,正确理解交集的概念。
直接写出答案。
易错点
本题易混淆并集与交集的概念,对集合的表示方法理解错误。
知识点
2.若复数



正确答案
解析
由题意得


考查方向
解题思路
本题考查了复数的模的概念,简单的运算能力。解题步骤如下:
写出复数模的计算公式。
由公式直接算出结果。
易错点
本题易忘记复数的模的概念和计算公式,出现计算错误。
知识点
3.从1,2,3,4这四个数中一次随机地取2个数,则所取2个数的乘积为偶数的概率是
正确答案
解析
随机地抽取2个数总可能数为6种,两个数之积为偶数的为:1,2;1,4;2,3;2,4;3,4,共有5种,那么所取的2个数之为偶数的概率为
考查方向
解题思路
本题考查了古典概型的求法,简单的运算推理能力。解题步骤如下:
写出基本事件的总数和满足条件的事件个数。
根据古典概型的计算公式,求出结果。
易错点
本题易混淆古典概型与几何概型的意义,对基本事件的个数会遗漏。
知识点
4.根据下图所示的伪代码,可知输出的结果S为
正确答案
21
解析
【解析】模拟执行程序,开始有I=1,S=0,此时满足条件S≤10;接下来有I=2,S=1,此时满足条件S≤10;接下来有I=3,S=1+4=5,此时满足条件S≤
考查方向
解题思路
本题主要考查伪代码,阅读能力.简单的推理运算能力。解题步骤如下:
从I=1开始一直循环到I=4
退出循环,输出结果。
易错点
本题容易出错的地方就是循环的结束的确定。
知识点
5.为了了解居民家庭网上购物消费情况,某地区调查了10000户家庭的月消费金额(单位:元),所有数据均在区间
正确答案
750.
解析
由题意得,被调查的10000户家庭中,消费额在1000元以下的户数有:(0.0001+0.00015)×500×10000=750户.
考查方向
解题思路
本题主要考查统计的概念,直方图等知识。解题步骤如下:
找出前面二个矩形的高度,即纵坐标。
利用公式求得结果。
易错点
本题易错点是看不懂直方图中矩形面积的意义,把1000元以下,理解为包含1000元。
知识点
6.设等比数列




正确答案
63.
解析
由等比数列前n项和的性质



设等比数列{an}的首项为a1,公比为q.显然q≠1,由题意得


考查方向
解题思路
本题主要考查等比数列的基本运算,等比数列的求和。解题步骤如下:
利用公式或性质,列出等式。
正确运算,得出结果。
易错点
本题易错点是公式会弄错,运算上出现错误。
知识点
9.若函数

正确答案

解析
因为函数f(x)为奇函数,所以
f(-1)=-f(1),f(-2)=-f(2),即

f(a+b)=f(1)=-1.
考查方向
解题思路
本题主要考查函数,分段函数的概念,函数的奇偶性,函数的求值等基础知识。解题步骤如下:
求出二次函数图像的顶点,利用奇函数的对称性质,列出方程。
解方程求出a,b,进一步求出结果。
易错点
本题易混淆奇函数与偶函数的图像的对称性质,不能正确利用奇函数的图像关于原点对称这一性质解决。
知识点
10.已知

正确答案

解析

所以
考查方向
解题思路
本题主要考查三角函数的基本性质,诱导公式,两角和与差三角函数,三角函数的恒等变换.解题步骤如下:
把未知角变换成已经角。
利用诱导公式和同角三角函数的基本关系式求解。
易错点
本题不容易想到角的变换,有时公式记错,导致结果错误。
知识点
7.在平面直角坐标系



正确答案

解析
由题意可得


考查方向
解题思路
本题主要考查双曲线的标准方程,双曲线几何性质,渐近线等概念。解题步骤如下:
由双曲线的性质和渐近线方程的概念列出方程组。
解方程组求出答案即可。
易错点
本题易混淆焦点在X轴与Y轴的双曲线的渐近线方程。
知识点
8.已知正方体



正确答案

解析
根据等体积法可得
考查方向
解题思路
本题主要考查多面体的概念,三棱锥的体积求法.解题步骤如下:
正确找到合适的点作为三棱锥的顶点。
利用公式计算得出结果。
易错点
本题用等体积法解决时,不能正确变换图形位置,即找不到用那个点为三棱锥的顶点。
知识点
12.已知边长为6的正三角形



则
正确答案
3.
解析



又B.P.E三点共线,






考查方向
解题思路
本题主要考查向量的线性运算,向量的数量积,向量的坐标运算。解题步骤如下:
由向量基本定理和B.P.E三点共线求出向量

利用数量积公式求出结果。
易错点
本题不容易想到利用B.P.E三点共线寻找突破口,不能正确运用向量的基本定理解决问题。
知识点
13.在平面直角坐标系



切点分别为


正确答案

解析
由题设函数y=x2在A(x1,y1)处的切线方程为:y=2x1 x-x12,
函数y=x3在B(x2,y2)处的切线方程为y=3 x22 x-2x23.
所以


所以
考查方向
解题思路
本题主要考
由导数几何意义,写出切线方程。
解方程组,得出答案。
易错点
本题易错的地方是不能正确理解导数的几何意义,以及导数公式记错。
知识点
11.在平面直角坐标系



使得

正确答案

解析
设满足条件PA=2PB的P点坐标为(x,y),则(x-4)2+y2=4(x-1)2+4y2,化简得
x2+y2=4.要使直线x-y+m=0有交点,则≤2.即-2≤m≤2.
考查方向
解题思路
本题主要考查直线与圆的位置关系,点到直线距离.解题步骤如下:
由已知条件,求出P点的轨迹方程。
利用直线与圆的位置关系解决。
易错点
本题易错点是找不到P点的轨迹是圆,从而不能利用直线与圆的位置关系解决。
知识点
14.已知函数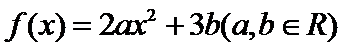
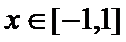
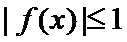
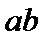
正确答案
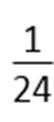
解析
由|f(x)|≤1,得|2a+3b|≤1,
所以,6ab≤|2a·3b|=|2a+3b-3b|·|3b|≤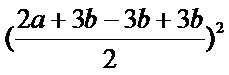
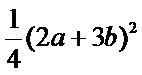
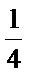
且当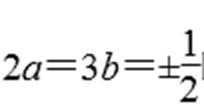
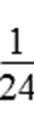
考查方向
解题思路
本题主要考查二次函数.函数性质.基本不等式.绝对值的概念.解题步骤如下:
由任意性,想到用端点值代入,得到不等式|2a+3b|≤1。
配凑出能使用基本不等式的式子。
易错点
本题不易想到使用基本不等式的配凑法,不能正确理解条件中的“任意”二字。
知识点
15.在



(1)求角
(2)若

正确答案
(1)
(2)
解析
试题分析:本题属于解三角形中的基本问题,难度不大。
(1)此类问题主要应用正(余)弦定理和三角形面积公式;(2)注意边和角的统一。
解析:(1)在△ABC中,由(a+b-c)(a+b+c)=ab,得

因为0<C<π,所以C=
(2)因为c=2acosB,由正弦定理,得
sinC=2sinAcosB,
因为A+B+C=π,所以sinC=sin(A+B),
所以sin(A
又-

所以A-B=0,即A=B,所以a=b=
所以△ABC的面积为
考查方向
解题思路
本题旨在考查三角函数的基本关系.正弦定理.余弦定理.三角形面积公式.向量的数量积等基本知识.解题步骤如下:
化简已知条件,利用余弦定理求解。
边角互化,利用正(余)弦定理和三角形面积公式求解。
易错点
第一问中化简易出错误。
第二问不知道统一成边或者角进行处理。
知识点
17.如图,在平面直角坐标系


离心率为
(1)求椭圆的方程;
(2)若直线






正确答案
(1)
(2)
解析
试题分析:此题是直线与圆锥曲线的常见题型,运算量较大。此类问题往往要用到韦达定理,设而不求等方法技巧,把几何关系转化为代数运算。
(1)由条件知椭圆

所以
又点A(2,1)在椭圆
所以
解得
所以,所求椭圆的方程为
(2)将

整理,得
由线段BC被y轴平分,得
因为

因为当


由方程①,得
又因为
所以


由于


所以,此时直线l的方程为
考查方向
解题思路
本题主要考查椭圆的标准方程和几何性质,直线与椭圆的交点,直线斜率等基础知识。解题步骤如下:
把点代入椭圆方程进而求出方程
把垂直关系转化为点的坐标运算。
易错点
第一问对椭圆中的a,b,c表示的意义不明确;
第二问中不能把垂直关系与二次方程的解和点的坐标结合起来考虑。
知识点
20.若数列

(1)已知数列

①求数列
②试判断数列
(2)已知数列


正确答案
(1)①
(2)略.
解析
试题分析:此题是结合等差(比)数列,给出新定义的创新试题,难度较大。在解题中要充分利用新定义的性质,合理推理,得出结论。
(1)①由an+1=2an-1,得an+1-1=2(an-1),且a1-1=1,
所以数列{an-1}是首项为1,公比为2的等比数列.
所以an-1=2n-1.
所以,数列{an}的通项公式为a n=2n-1+1.
②数列{an}不是“等比源数列”.用反证法证明如下:
假设数列{an}是“等比源数列”,则存在三项am,an,ak (m<n<k)按一定次序排列构成等比数列.
因为an=2n-1+1,所以am<an<ak.
所以an2=am·ak,得 (2n-1+1)2=(2m-1+1)(2k-1+1),即22n-m-1+2n-m+1-2k-1-2k-m=1.
又m<n<k,m,n,k∈N*,
所以2n-m-1≥1,n-m+1≥1,k-1≥1,k-m≥1.
所以22n-m-1+2n-m+1-2k-1-2k-m为偶数,与22n-m-1+2n-m+1-2k-1-2k-m=1矛盾.
所以,数列{an}中不存在任何三项,按一定次序排列构成等比数列.
综上可得,数列{an}不是“等比源数列”.
(2)不妨设等差数列{an}的公差d≥0.
当d=0时,等差数列{an}为非零常数数列,数列{an}为“等比源数列”.
当d>0时,因为an∈Z,则d≥1,且d∈Z,所以数列{an}中必有一项am>0.
为了使得{an}为“等比源数列”,
只需要{an}中存在第n项,第k项(m<n<k),使得an2=amak成立,
即[am+(n-m)d]2=am[am+(k-m)d],即(n-m)[2am+(n-m)d]=am(k-m)成立.
当n=am+m,k=2am+amd+m时,上式
所以,数列{an}为“等比源数列”.
考查方向
解题思路
本题主要考查数列的概念.等差数列.等比数列的的通项公式与求和公式.不等式的求解等基本性质.解题步骤如下:
根据已知条件构造新数列,从而求出数列的通项a n;
利用等差(比)数列的性质,和题目给出的新定义“等比源数列”进行合理的恒等变换和推理,得出解答。
易错点
不能正确理解题目中给出的新定义“等比源数列”
在判断“等比源数列”中的恒等变换时易出错。
知识点
16.如图,在直四棱柱



求证:(1)
(2)

正确答案
(1)略;(2)略.
解析
试题分析:此题属于立体几何中的线面关系的位置关系的证明题,难度不大,只要熟悉了线面关系中平行与垂直的判定和性质定理,即可完成。
(1)在直四棱柱ABCD–A1B1C1D1中,
连结BD交AC于点F,连结B1D1交A1C1于点E.
因为四边形ABCD是菱形,所以BD⊥AC.
因为ABCD–A1B1C1D1为直棱柱,
所以BB1⊥平面ABCD,又AC
所以,BB1⊥AC.
又BD∩BB1=B,BD

所以AC⊥平面B1BDD1.
而BE
(2)连结D1F,因为四棱柱ABCD–A1B1C1D1为直棱柱,
所以四边形B1BDD1为矩形.

所以BF=D1E,且BF∥D1E.
所以四边形BED1F是平行四边形.
所以BE∥D1F.
又D1F

所以 BE∥平面ACD1.
考查方向
解题思路
本题主要考查直线与直线.直线与平面及平面与平面的位置关系等基础知识。解题步骤如下:
由线面垂直推出线线垂直;
由线线平行推出线面平行。
易错点
第一问在书写时易遗漏BD∩BB1=B这一条件;
第二问在书写时易遗漏D1F

知识点
18.如图,阴影部分为古建筑物保护群所在地,其形状是以










(1)按下列要求建立函数关系:
①设



②设



(2)请你选用(1)中的一个函数关系,求

正确答案
(1)①

(2)
解析
试题分析:此类问题是典型的函数建模问题,难度较大。解决的关键是把实际问题转化为函数问题进行求解。
(1)①由题设知,在Rt△O1PT中,
∠OPT=


又OO1=1,所以OP
在Rt△OPQ中,

所以,Rt△OPQ的面积为

②由题设知,OQ= QT = t,O1T=1,且Rt△POQ∽Rt△PT O1,
所以

化简,得
所以,Rt△OPQ的面积为

(2)选用(1)中①的函数关系

由

列表
所以,当

(2)选

由

列表
所以,当

考查方向
解题思路
本题主要考查直线.圆.解三角形等基础知识。解题步骤如下:
根据已知条件,合理建立函数关系式;
利用导数求出函数的最值。
易错点
第一问不能正确读懂题意,因而无法下手;
第二问得出函数关系后,不知道用导数解决最值问题。
知识点
19.已知函数
(1)求函数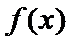
(2)试求函数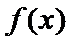
正确答案
(1)函数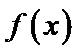
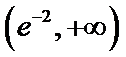
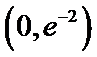
(2)当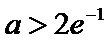
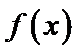
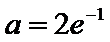
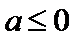
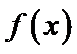
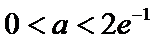
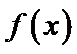
解析
试题分析:此题属于导数的常规问题,难度较大。函数的单调性,最值,零点的个数等等,都可利用导数加以解决。
(1)由函数f(x)=a+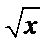
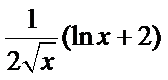
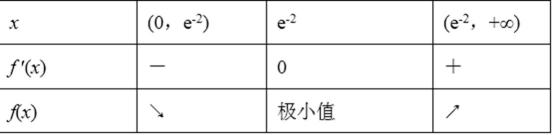
令f ′(x)=0,得 x=e-2.列表如下:
因此,函数f(x)
(2)由(1)可知,fmin(x)=f(e-2)=a-2e-1.
(i)当a>2e-1时,由f(x)≥f(e-2)=a-2e-1>0,得函数f(x)的零点个数为0.
(ii)当a=2e-1时,因f(x)在(e-2,+∞)上是单调增,在(0,e-2)上单调减,
故x∈(0,e-2)∪(e-2,+∞)时,f(x)>f(e-2)=0.
此时,函数f(x)的零点个数为1.
(iii)当a<2e-1时,fmin(x)=f(e-2)=a-2e-1<0.
①a≤0时,
因为当x∈(0,e-2]时,f(x)=a+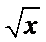
所以,函数f(x)在区间(0,e-2]上无零点;
另一方面,因为f(x)在[e-2,+∞)单调递增,且f(e-2)=a-2e-1<0,
又e-2a∈(e-2,+∞),且f(e-2a)=a(1-2e-a)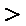
此时,函数f(x)在(e-2,+∞)上有且只有一个零点.
所以,当a≤0时,函数f(x)零点个数为1.
②0<a<2e-1时,
因为f(x)在[e-2,+∞)上单调递增,且f(1)=a>0,f(e-2)=a-2e-1<0,
所以,函数f(x)在区间(e-2,+∞)有且只有1个零点;
另一方面,因为f(x)在(0,e-2]上是单调递减,且f(e-2)=a-2e-1<0
又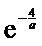
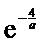
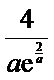
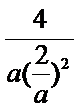
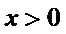
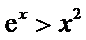
此时,函数f(x)在(0,e-2)上有且只有1个零点.
所以,当0<a<2e-1时,函数f(x)零点个数为2.
综上所述,当a>2e-1时,f(x)的零点个数为0;当a=2e-1,或a≤0时,f(x)的零点个数为1;
当0<a<2e-1时,f(x)的零点个数为2.
考查方向
解题思路
本题主要考查函数的基本性质.导数的应用等基础知识。解题步骤如下:
求出导数,考察导数在指定区间上的正负号,从而得出函数的单调性;
把考察零点个数问题转化为函数的最值问题来解决。
易错点
第一问不能正确判断导函数在指定区间的正负号;
第二问不能理解考察零点的个数,可以转化为最值问题来处理。