文科数学三明市2013年高三试卷

精品

单选题
填空题
简答题

立即下载

文科数学热门试卷

X 查看更多试卷

试卷目录

1、单选题

2、填空题

3、简答题

真题试卷
模拟试卷
预测试卷

单选题本大题共12小题，每小题5分，共60分。在每小题给出的4个选项中，有且只有一项是符合题目要求。

题型：单选题

分值: 5分

1. 已知集合，,则等于（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

集合的含义

题型：单选题

分值: 5分

2.若，, 则（）

A（1，1）

B（－1，－1）

C（3，7）

D（-3,-7）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

向量的减法及其几何意义

题型：单选题

分值: 5分

5. 方程的解所在的区间是（）

A（0,1）

B（1,2）

C（2,3）

D（3,4）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

函数的单调性及单调区间

题型：单选题

分值: 5分

10．若一个底面是正三角形的三棱柱的正视图如图所示，其侧视图面积等于（　）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

空间几何体的结构特征

题型：单选题

分值: 5分

11．已知是定义在R上的奇函数，且当时，，则=（）

C-1

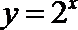
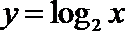
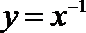
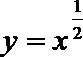
正确答案

解析

解析已在路上飞奔，马上就到！

知识点

函数的概念及其构成要素

题型：单选题

分值: 5分

3. ＂＂是＂＂的（　　）

A充分不必要条件

B必要不充分条件

C充要条件

D既不充分也不必要条件

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

四种命题及真假判断

题型：单选题

分值: 5分

4、已知四个函数：①；②；③；④。则下列函数图象（在第一象限部分）从左到右依次与函数序号的正确对应顺序是（）

A②①③④

B②③①④

C④①③②

D④③①②

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

四种命题及真假判断

题型：单选题

分值: 5分

6．已知正整数满足，则使得取得最小值的有序数对是（　　）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

利用基本不等式求最值

题型：单选题

分值: 5分

7. 某几何体的三视图如图所示，它的体积为( )

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

空间几何体的结构特征

题型：单选题

分值: 5分

9．平面向量与的夹角为，,，则（）

D12

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

空间几何体的结构特征

题型：单选题

分值: 5分

12. 设直线与函数，的图象分别交于点，则当达到最小时的值为（　　）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

函数的概念及其构成要素

题型：单选题

分值: 5分

8．已知等比数列的前项和为，且，则数列的公比的值为（）

A-2

C-1或2

D1或-2

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

等比数列的基本运算

填空题本大题共4小题，每小题4分，共16分。把答案填写在题中横线上。

题型：填空题

分值: 4分

13.设=__________

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

函数的概念及其构成要素

题型：填空题

分值: 4分

14．已知和是非零向量,且与的夹角为,则向量的模为___________

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

空间几何体的结构特征

题型：填空题

分值: 4分

15．若函数图象上存在点满足约束条件，则实数的最大值为 ________

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

函数的图象与图象变化

题型：填空题

分值: 4分

16．下列说法中：

①函数与的图象没有公共点；

②若定义在上的函数满足，则6为函数的周期；

③若对于任意，不等式恒成立，则；

④定义：“若函数对于任意，都存在正常数，使恒成立，则称函数为有界泛函．”

由该定义可知，函数为有界泛函。则其中正确的是_____________

正确答案

①②

解析

解析已在路上飞奔，马上就到！

知识点

函数的概念及其构成要素

简答题（综合题）本大题共74分。简答应写出文字说明、证明过程或演算步骤。

题型：简答题

分值: 12分

18．已知，，且

（Ⅰ）求与的夹角；

（Ⅱ）求的值。

正确答案

（Ⅰ）

∴，

∵，

∴

（Ⅱ）∵，

∴

解析

解析已在路上飞奔，马上就到！

知识点

空间几何体的结构特征

题型：简答题

分值: 12分

17. 在等差数列中，

（Ⅰ）求该等差数列的通项公式；

（Ⅱ）若为数列的前项和，求。

正确答案

（Ⅰ）设等差数列的首项为，公差为，

则,

解得：所以，

（Ⅱ），

所以

解析

解析已在路上飞奔，马上就到！

知识点

由数列的前几项求通项

题型：简答题

分值: 12分

19． △ABC中，角A、B、C的对边分别为a、b、c，且，

（Ⅰ）求角A的大小；

（Ⅱ）若，求△ABC的面积。

正确答案

（Ⅰ）从已知条件得

（Ⅱ）由余弦定理

代入b+c=4得bc=3

故△ABC面积为

解析

解析已在路上飞奔，马上就到！

知识点

任意角的概念

题型：简答题

分值: 12分

20．如图，四面体中，与都是边长为4的正三角形。

（I）求证：；

（II）试问该四面体的体积是否存在最大值？若存在，求出这个最大值及此时棱长的大小；若不存在，说明理由。

正确答案

(Ⅰ)

证明　取的中点，连接，

∵与都是边长为4的正三角形，

∴，。

又∵，

∴平面。又平面，

∴。

(Ⅱ)解：由已知得，为等腰三角形，且，

设，为棱的中点，则，

·=·

当，即时，，

∴该四面体存在最大值，最大值为8，

此时棱长。

解析

解析已在路上飞奔，马上就到！

知识点

空间几何体的结构特征

题型：简答题

分值: 12分

21．若实数满足，则称比远离。

（Ⅰ）若比1远离0，求的取值范围；

（Ⅱ）已知函数的定义域。任取，等于和中远离0的那个值．写出函数的解析式，并指出它的基本性质（结论不要求证明）。

正确答案

（I）根据定义可得：，或

（Ⅱ）

解析

解析已在路上飞奔，马上就到！

知识点

函数解析式的求解及常用方法正弦函数的图象余弦函数的图象绝对值不等式的解法

题型：简答题

分值: 14分

22．已知函数在处取得极值2。

(Ⅰ)求函数的解析式；

(Ⅱ)若函数在区间上是单调函数，求实数的取值范围；

(Ⅲ)设函数，若对于任意的,总存在，使得，求实数的取值范围。

文科数学 热门试卷

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

文科数学热门试卷