- 真题试卷
- 模拟试卷
- 预测试卷
2. 若



正确答案
解析


考查方向
解题思路
先化简复数,然后对应项相等求解。
易错点
忽略
知识点
3. 设




正确答案
解析
因为
即,
考查方向
解题思路
利用等差数列
易错点
等差数列项和项数的关系
知识点
4. 已知双曲线

正确答案
解析
通过离心率求渐近线
考查方向
解题思路
根据离心率的值建立a与c的关系,进而找到渐近线的方程。
易错点
离心率与渐近线方程记错
知识点
6. 以下四个命题中,真命题的个数是( )
① 若



② 

③ 
④ 函数


正确答案
解析
1对,2对,3 对,第4个错误
考查方向
解题思路
按照相关的概念,依次判断
易错点
重要条件的判断
知识点
8. 在半径为2的圆内的一条直径上任取一点,过这个点作垂直该直径的弦,则弦长超过圆内接正三角形边长的概率是( )
正确答案
解析
设圆的半径为r,
圆心为O,
AB为圆的一条直径,
CD为垂直于AB的一条弦,垂足为M,
若CD为圆内接正三角形的一条边,则O到CD的距离为r/2,
设EF为与CD平行且到圆心O距离为r/2的弦,
交直径AB于点N,所以当过AB上的点且垂直于AB的弦的长度超过CD时,
该点在线段MN上移动,所以所求概率P=r/2r=1/2,所以选C
考查方向
解题思路
找到弦长于圆内接正三角形边长的情况
易错点
找临界值
知识点
10. 已知一个几何体的三图如图所示,则该几何体的体积为( )
正确答案
解析
几何体的体积公式利用底面积乘以高求得,所以选D
考查方向
解题思路
本题考查由三视图还原几何体并且看出几何体各个部分的长度,本题解题的关键是要求体积需要求出几何体的底面面积和高,三棱锥的高是由垂直与底面的侧面的高得到,本题是一个基础题.
易错点
立体感不强
知识点
11. 已知函数


正确答案
解析


所以答案为50,选择A
考查方向
解题思路
先求出通项公式an,然后两项一组,即可求解数列的钱50项和
易错点
通项公式不会求
知识点
1. 已知全集



正确答案
解析
集合A中的代表元素为x,x的取值范围为


考查方向
解题思路
理解集合A和集合B中元素的特点
易错点
集合中元素的特征,集合A表示的意义
知识点
5. 执行图中的程序框图(其中


正确答案
解析
n=0不满足判断框中的条件,n=1,s=1;
n=1不满足判断框中的条件,n=2,s=2 ;
n=2不满足判断框中的条件,n=3,s=3
n=3不满足判断框中的条件,n=4,s=5
n=4不满足判断框中的条件,n=1,s=7
n=5不满足判断框中的条件,n=5,s=9
n=5满足判断框中的条件,输出的结果为9,所以答案为C
考查方向
解题思路
顺序结构 循环结构 判断结构
易错点
循环语句理解错误,判断条件看错
知识点
9. 若点P在抛物线
正确答案
解析
由已知条件,利用两点间的距离公式,求出|PQ|,
因为点P是抛物线
设p
所以
即
所以当

最小值为
考查方向
解题思路
找到|PQ|的表达式,然后求最值
易错点
抛物线的相关性质
知识点
12. 若函数

正确答案
解析
因为
所以
另
所以
所以可得


所以结合选项,b的取值范围为
考查方向
解题思路
先根据导函数在区间上有零点,得到b的取值范围,再利用b的取值范围,求出函数的单调区间,结合题目,选择正确的选项
易错点
判断b的取值范围,
知识点
7. 定义






正确答案
解析
根据矩阵的定义,可以得到
所以
所以图象向右平移可得,
所以选A
考查方向
解题思路
先根据矩阵的定义,得到f(x)的解析式,然后根据函数的解析式平移可得
易错点
三角函数公式记忆混淆
知识点
13. 已知



正确答案
解析
因为向量b与向量c平行,
所以s=(-1)*2=-2.
所以
所以答案为
考查方向
解题思路
先根据向量平行求解出s的值,进而求出余弦值
易错点
向量平行的计算
知识点
14. 已知变量


正确答案
10
解析
如图所示,根据约束函数画出可行域,则A点为最大值,A(1,3)所以
考查方向
解题思路
先根据约束条件,作出正确的可行域
易错点
作图错误,找不到最大值的点
知识点
15. 在四棱锥



正确答案
解析
根据已知条件,可求外接球的半径为
所以表面积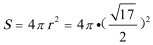
所以表面积为
考查方向
解题思路
先根据已知条件求外接球的半径,然后根据表面积公式求外接球的表面积
易错点
求外接球的半径
知识点
16. 若定义在区间





①



⑤

正确答案
①④⑤
解析
第1个,
第4个
第5个在定义域内有最值,,其余都不是有界的,所以此题选择①④⑤
考查方向
解题思路
根据定义,一依次判断
易错点
不能运用新定义的概念的性质去解题
知识点
17.在



(Ⅰ)求证:
(Ⅱ)若


正确答案
见解析
解析
(Ⅰ)
证明:由正弦定理得:
即

(Ⅱ)


考查方向
解题思路
第一问根据正弦定理得到三个角的正弦关系,进而建立角与边的关系,第二问利用正弦定理求面积公式求解
易错点
正弦定理误用、化简整理错误
知识点
18.某校对高一年级学生寒假参加社区服务的次数进行了统计,随机抽取了M名学生作为样本,得到这M名学生参加社区服务的次数,根据此数据作出了频率分布统计表和频率分布直方图如下:
(Ⅰ)求表中n, p的值和频率分布直方图中
(Ⅱ)如果用分层抽样的方法从样本服务次数在[10,15)和[25,30)的人中共抽取6人,再从这6人中选2人,求2人服务次数都在[10,15)的概率.
正确答案
见解析
解析
(Ⅰ)
因20÷



中位数位于区间
则0.125x=0.25,所以x=2,所以学生参加社区服务次数的中位数为17次。
(Ⅱ)
由题意知样本服务次数在[10,15)有20人,样本服务次数在[25,30)有4人. 如果用分层抽样的方法从样本服务次数在[10,15)和[25,30)的人中共抽取6人,则抽取的服务次数在[10,15)和[25,30)的人数分别为:

记服务次数在[10,15)为

从已抽取的6人中任选两人的所有可能为:
共15种.设“2人服务次数都在[10,15)”为事件

共10种,
所以
考查方向
解题思路
根据表和图的信息,仔细求解
易错点
作图,遗漏数据
知识点
19.(本小题满分12分)如图,已知四棱锥


(Ⅰ)证明:
(Ⅱ)若

正确答案
见解析
解析
(Ⅰ)
证明:取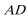





又






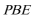

(Ⅱ)
由(Ⅰ)






由侧面





考查方向
解题思路
作出适当的辅助线,根据线面垂直证明线线垂直
易错点
找垂直条件时找不到
知识点
20.已知椭圆



(Ⅰ)求椭圆
(Ⅱ)若斜率为







正确答案
见解析
解析
(Ⅰ)
设1
由抛物线







(Ⅱ)
设





当



考查方向
解题思路
根据已知条件,建立各种方程关系,代入整理求解。
易错点
计算错误
知识点
21.已知函数
(Ⅰ)讨论函数
(Ⅱ)若对任意不相等的


正确答案
见解析
解析
(Ⅰ)
(Ⅱ)
不妨设




令

即就是
令
考查方向
解题思路
求出函数的定义域,求导函数,判断单调区间,构造恰当的函数,结合不等式关系,求出参数的取值范围。
易错点
求导错误、对参数的分类讨论
知识点
22.已知









(Ⅰ)求证:
(Ⅱ)若




正确答案
见解析
解析
(Ⅰ)
证明:












(Ⅱ)






在Rt




在Rt


考查方向
解题思路
根据条件、认真推理
易错点
对概念性质理解不透彻