文科数学合肥市2011年高三试卷

精品

单选题
填空题
简答题

立即下载

文科数学热门试卷

X 查看更多试卷

试卷目录

1、单选题

2、填空题

3、简答题

真题试卷
模拟试卷
预测试卷

单选题本大题共10小题，每小题5分，共50分。在每小题给出的4个选项中，有且只有一项是符合题目要求。

题型：单选题

分值: 5分

1．已知集合，，且M，N都是全集I的子集，则图中阴影部分表示的集合为（）

A{-1，-2，-3}

B{0，1，2，3}

C{2，3}

D{0，-1，-2，-3}

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

导数的乘法与除法法则

题型：单选题

分值: 5分

3．已知向量m，n的夹角为，且=（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

导数的乘法与除法法则

题型：单选题

分值: 5分

6．已知圆，直线，则圆C上的点到直线的距离最小值为（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

指数函数的图像变换

题型：单选题

分值: 5分

5．函数的图像如图所示，则函数的图像大致是（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

对数函数的图像与性质知图选式与知式选图问题

题型：单选题

分值: 5分

2．i是虚数单位，在复平面上对应的点位于（）

A第一象限

B第二象限

C第三象限

D第四象限

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

复数的代数表示法及其几何意义复数代数形式的乘除运算

题型：单选题

分值: 5分

4．一个几何体的三视图如图所示，则该几何体的表面积等于（）

A8π

B9π

C10π

D11π

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

幂函数的概念、解析式、定义域、值域

题型：单选题

分值: 5分

7．阅读如图所示的程序框图，若输入，则输出的值分别为（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

指数函数的图像变换

题型：单选题

分值: 5分

8．各项均为正数的等比数列的公比成等差数列，则=（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

指数函数的单调性与特殊点

题型：单选题

分值: 5分

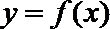
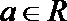
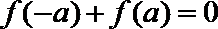
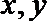
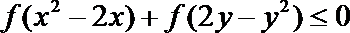
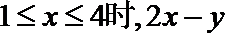
10．定义在R上的函数是减函数，且对任意的，都有，若满足不等式，则当的最大值为（）

B10

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

奇偶性与单调性的综合二次函数在闭区间上的最值

题型：单选题

分值: 5分

9．已知直线，函数的图象与直线相切于P点，若，则P点的坐标可能是（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

幂函数的概念、解析式、定义域、值域

填空题本大题共5小题，每小题5分，共25分。把答案填写在题中横线上。

题型：填空题

分值: 5分

11．若命题“”是真命题，则a的取值范围是___________。

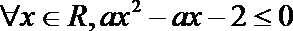
正确答案

-8≤a≤0

解析

解析已在路上飞奔，马上就到！

知识点

充要条件的应用

题型：填空题

分值: 5分

12．空间直角坐标系O—xyz中，球心坐标为（-2，0，3），半径为4的球面方程是___________。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

平行关系的综合应用

题型：填空题

分值: 5分

14．抛物线的焦点与双曲线的上焦点重合，则m=___________。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

复合函数的单调性

题型：填空题

分值: 5分

13．某单位为了制定节能减排的目标，先调查了用电量y（度）与气温x（°C）之间的关系，随机统计了某4天的用电量与当天气温，并制作了对照表：

由表中数据，得线性回归方程，当气温为-5°C时，预测用电量的度数约为___________度。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

指数函数的单调性与特殊点

题型：填空题

分值: 5分

15．给出以下结论：

①甲从四面体中任意选择一条棱，乙也从该四面体中任意选择一条棱，则所得的两条棱所在的直线是异面直线的概率是

②关于x的不等式恒成立，则a的取值范围是

③若关于x的方程上没有实数根，则k的取值范围是；

④函数有一个零点。

其中正确的结论是___________（填上所有正确结论的序号）

正确答案

①④

解析

解析已在路上飞奔，马上就到！

知识点

命题的真假判断与应用函数零点的判断和求解不等式恒成立问题古典概型的概率

简答题（综合题）本大题共75分。简答应写出文字说明、证明过程或演算步骤。

题型：简答题

分值: 12分

16．已知函数，且函数的图像的一个对称中心为

（I）求a和函数的单调递减区间；

（II）在三角形ABC中，角A，B，C的对边分别是a，b，c，满足，求函数的取值范围。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

利用导数证明不等式

题型：简答题

分值: 12分

17．合肥一中为了了解学校食堂的服务质量情况，对在校就餐的1400名学生按5%的比例进行问卷调查，把学生对食堂的“服务满意度”与“价格满意度”都分为五个等级：1级（很不满意）；2级（不满意）；3级（一般）；4级（满意）；5级（很满意），其统计结果如下表所示（服务满意度为x，价格满意度为y）。

（I）作出“价格满意度”的频率分布直方图；

（II）求“服务满意度”为3时的5个“价格满意度”数据的标准差；

（III）为改进食堂服务质量，现从的五人中抽取两人征求意见，求至少有一人的“服务满意度”为1的概率。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

指数函数的图像变换

题型：简答题

分值: 12分

18．已知直线的方程为，数列的前n项和为，点在直线上。

（I）求数列的通项公式；

（II），数列的前n项和为的最大值。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

函数单调性的性质

题型：简答题

分值: 13分

20．已知函数

（I）求函数的单调区间和极值；

（II）若均有，求实数a的取值范围。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

幂函数的概念、解析式、定义域、值域

题型：简答题

分值: 13分

21．已知圆，点C2（1，0），点Q在圆C1上运动，QC2的垂直平分线交QC1于点P。

（I）求动点P的轨迹W的方程；

（II）设M，N是曲线W上的两个不同点，且点M在第一象限，点N在第三象限，若为坐标原点，求直线MN的斜率k；

（III）过点且斜率为k的动直线交曲线W于A，B两点，在y轴是否存在定点D，使以AB为直径的圆恒过这个点？若存在，求出D的坐标，若不存在，说明理由。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

二元二次方程表示圆的条件

题型：简答题

分值: 13分

19．如图，正三棱锥ABC—A1B1C1中，AB=2，AA1=1，D是BC的中点，点P在平面BCC1B1内，PB1=PC1=2。

（I）求证：；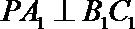

（II）求证：PB1//平面AC1D；

（III）求多面体PA1B1DAC1的体积。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

幂函数的图像

文科数学 热门试卷

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

文科数学热门试卷