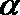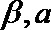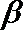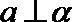- 真题试卷
- 模拟试卷
- 预测试卷
下列有关固定化酶和固定化细胞的叙述,正确的是
正确答案
解析
固定化技术包括包埋法、物理吸附法和化学结合法(交联法),由于细胞相对于酶来说更大,难以被吸附或结合,因此多采用包埋法, A正确;某些反应产物可能与酶结合,致使酶的结构产生变化,从而改变酶的催化活性,B错误;固定化酶实质上是将相应酶固定在不溶于水的载体上,实现酶的反复利用,并提高酶稳定性,酶的各项特性(如高效性、专一性和作用条件的温和性)依然保持,C错误;固定化细胞在多步酶促反应中发挥连续催化作用,但如果反应底物是大分子物质,则难以自由通过细胞膜,从而限制固定化细胞的催化反应,D错误。
知识点
1.定义


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6. 将函数



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5. 一个几何体的三视图如图所示,则这个几何体的体积为( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2.下列命题中,真命题是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.设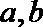
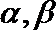
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.某程序框图如图所示,该程序运行后输出的结果为( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.已知函数

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.在平面直角坐标系





①该函数的值域为
②该函数图象关于原点对称;
③该函数图象关于直线
④该函数的单调递增区间为
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.已知数列


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.已知等差数列










正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.如图,过抛物线







正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12.对于函数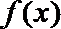
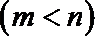
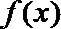
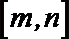
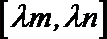
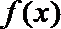
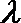
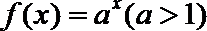
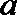
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14.若向量


正确答案
0
解析
解析已在路上飞奔,马上就到!
知识点
16.已知正方体





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
13.已知函数

正确答案
0
解析
解析已在路上飞奔,马上就到!
知识点
15.已知变量


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17. 等比数列 





(1)求数列 
(2)若数列 



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18. 已知向量


(1)求函数
(2)在







正确答案
(1)
对称中心为
(2) 

∴
∴
∴
即:
将

解之得:
∴


解析
解析已在路上飞奔,马上就到!
知识点
21. 如图,已知点











(1)求椭圆
(2)求证:直线

正确答案
(1)由题意,可得



解得


所以椭圆

(2)证明:设直线





由
所以


设直线



则

将①、②式代入(*),
整理得
所以


解析
解析已在路上飞奔,马上就到!
知识点
19. 如图, 四棱柱




(1)证明: 

(2)求三棱柱
正确答案
(1)证明
在RT△
在RT△
(2)
解析
解析已在路上飞奔,马上就到!
知识点
22. 已知函数
(1)求函数

(2)若


(3)若在



正确答案
(1)
(2)
∵
∴



∴m的取值范围是
(3)构造
则转化为:若在



解析
解析已在路上飞奔,马上就到!