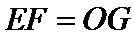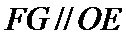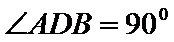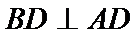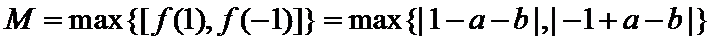- 真题试卷
- 模拟试卷
- 预测试卷
1.已知集合


正确答案
解析

考查方向
解题思路
先求出集合B,再求交集。
易错点
本题容易审错题意,误求并集,忽略集合B中代表元素及
知识点
2.甲、乙两人下棋,两人下成和棋的概率是

正确答案
解析
试题分析:甲不输的概率为
考查方向
解题思路
概率问题的考查,侧重于对古典概型和对立事件的概率考查,属于简单题.运用概率加法的前提是事件互斥,不输包含
易错点
本题容易审错题意,误求并集,忽略集合B中代表元素及
知识点
3.将一个长方形沿相邻三个面的对角线截去
正确答案
解析
试题分析:由题意得截去的是长方体前右上方顶点,故选B
考查方向
解题思路
解答此类题目的关键是由多面体的三视图想象出空间几何体的形状并画出其直观图,三视图中“正侧一样高、正俯一样长、俯侧一样宽”,因此,可以根据三视图的形状及相关数据推断出原几何图形中的点、线、面之间的位置关系及相关数据.本题直接用排除法进行判断即可。
易错点
忽略三视图中线的虚实导致出错。
知识点
7.已知△ABC是边长为1的等边三角形,点





正确答案
解析
试题分析:设





考查方向
解题思路
研究向量数量积,一般有两个思路,一是建立直角坐标系,利用坐标研究向量数量积;二是利用一组基底表示所有向量,两种实质相同,坐标法更易理解和化简.本题首先选好基底,然后用向量的记法及数量积德运算法则进行计算即可求出
易错点
不能熟知向量数量积的运算公式导致出错。
教师点评
向量数量积
【名师点睛】研究向量数量积,一般有两个思路,一是建立直角坐标系,利用坐标研究向量数量积;二是利用一组基底表示所有向量,两种实质相同,坐标法更易理解和化简. 平面向量的坐标运算的引入为向量提供了新的语言——“坐标语言”,实质是“形”化为“数”.向量的坐标运算,使得向量的线性运算都可用坐标来进行,实现了向量运算完全代数化,将数与形紧密结合起来.
知识点
8.已知函数




正确答案
解析
试题分析:



考查方向
解题思路
先根据三角恒等变换公式化简函数解析式,再根据零点求出x的值,进而求出
易错点
在化简函数解析式时容易出错。
知识点
4.已知双曲线


正确答案
解析
试题分析:由题得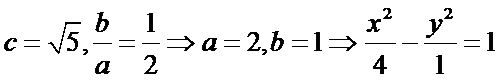
考查方向
解题思路
直接根据双曲线的性质即可求出双曲线的标准方程.
易错点
对双曲线的定义记忆不清楚导致出错。
知识点
5.设



正确答案
解析
试题分析:

考查方向
解题思路
直接根据充分、必要条件的三种判断方法进行判断.
易错点
对充分、必要条件的三种判断方法不清楚导致出错。
知识点
6.已知






正确答案
解析
试题分析:由题意得
考查方向
解题思路
直接根据函数的性质进行判断.
易错点
对充分、必要条件的三种判断方法不清楚导致出错。
知识点
9.i是虚数单位,复数


正确答案
1
解析
试题分析:

考查方向
解题思路
对于复数的四则运算,要切实掌握其运算技巧和常规思路,如






易错点
相关知识点不熟悉导致出错。
知识点
10.已知函数


正确答案
3
解析
试题分析:
考查方向
解题思路
直接根据求导法则求出函数的导数,然后即可求出
易错点
求导数是由于求导法则记忆错误导致出错。
知识点
11.阅读右边的程序框图,运行相应的程序,则输出
正确答案
4
解析
试题分析:第一次循环:


考查方向
解题思路
算法与流程图的考查,侧重于对流程图循环结构的考查.先明晰算法及流程图的相关概念,包括选择结构、循环结构、伪代码,其次要重视循环起点条件、循环次数、循环终止条件,更要通过循环规律,明确流程图研究的数学问题,是求和还是求项,本题直接按照程序逐步列出运行结果。
易错点
不知何时终止循环导致出错。
知识点
12.已知圆C的圆心在x轴的正半轴上,点


正确答案
解析
试题分析:设

考查方向
解题思路
根据题意设出圆的方程,利用点到直线的距离公式即可求出半径,进而求出远的方程。
易错点
忽略圆心在x轴的正半轴上导致出错。
知识点
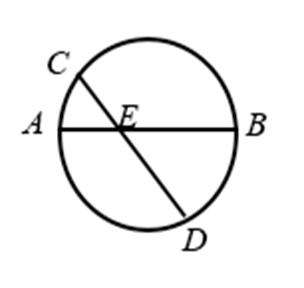
13.如图,AB是圆的直径,弦CD与AB相交于点E,BE=2AE=2,BD=ED,则线段CE的长为__________.
正确答案
解析
试题分析:设
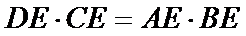
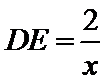


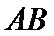


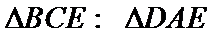
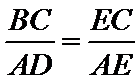
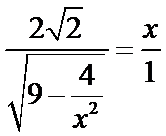
考查方向
解题思路
应用相交弦定理、切割线定理要抓住几个关键内容:如线段成比例与相似三角形、圆的切线及其性质、与圆有关的相似三角形等.本题根据相交弦定理即可求出CE长。
易错点
对相关定理不熟悉导致本题失分。
知识点
14. 已知函数


正确答案
解析
试题分析:由函数




考查方向
解题思路
根据函数的单调性先求出

易错点
不知如何应用已知条件
知识点
在


15.求B;
16.若
正确答案
(Ⅰ)
解析
试题分析:本题属于三角恒等变换与正弦定理的综合应用问题,属于简单题,解三角函数题,首先从角进行分析,善于用已知角表示所求角,即注重角的变换.角的变换涉及诱导公式、同角三角函数关系、两角和与差公式、二倍角公式、配角公式等,选用恰当的公式,是解决三角问题的关键,明确角的范围,对开方时正负取舍是解题正确的保证.本题只要掌握相关的公式及性质,即可解决本题,具体解析如下:
试题解析:(Ⅰ)解:在






考查方向
解题思路
(Ⅰ)利用正弦定理,将边化为角:

易错点
忽略角的范围导致出现增解。
正确答案
(Ⅱ)
解析
试题分析:本题属于三角恒等变换与正弦定理的综合应用问题,属于简单题,解三角函数题,首先从角进行分析,善于用已知角表示所求角,即注重角的变换.角的变换涉及诱导公式、同角三角函数关系、两角和与差公式、二倍角公式、配角公式等,选用恰当的公式,是解决三角问题的关键,明确角的范围,对开方时正负取舍是解题正确的保证.本题只要掌握相关的公式及性质,即可解决本题,具体解析如下:
(Ⅱ)解:由


考查方向
解题思路
(Ⅱ)问题为“已知两角,求第三角”,先利用三角形内角和为

易错点
忽略角的范围导致出现增解。
某化肥厂生产甲、乙两种混合肥料,需要A,B,C三种主要原料.生产1车皮甲种肥料和生产1车皮乙中肥料所需三种原料的吨数如下表所示:
现有A种原料200吨,B种原料360吨,C种原料300吨,在此基础上生产甲乙两种肥料.已知生产1车皮甲种肥料,产生的利润为2万元;生产1车皮乙种肥料,产生的利润为3万元.分别用x,y表示生产甲、乙两种肥料的车皮数.
17.用x,y列出满足生产条件的数学关系式,并画出相应的平面区域;
18.问分别生产甲、乙两种肥料各多少车皮,能够产生最大的利润?并求出此最大利润.
正确答案
(Ⅰ)解:由已知

解析
试题分析:本题属于线性规划的实际应用问题,主要考察了用二元线性规划的基础知识和基本方法解决简单实际问题的能力,以及概括能力和运算求解能力,属于简单题,解线性规划应用问题的一般步骤是:(1)分析题意,设出未知量;(2)列出线性约束条件和目标函数;(3)作出可行域并利用数形结合求解;(4)作答.而求线性规划最值问题,首先明确可行域对应的是封闭区域还是开放区域、分界线是实线还是虚线,其次确定目标函数的几何意义,是求直线的截距、两点间距离的平方、直线的斜率、还是点到直线的距离等等,最后结合图形确定目标函数最值取法.本题只要画对可行域,明确目标函数的意义即可解决,解析如下:
试题解析:(Ⅰ)解:由已知

考查方向
解题思路
(Ⅰ)根据生产原材料不能超过A种原料200吨,B种原料360吨,C种原料300吨,列出不等式关系式,即可行域,再根据直线及区域画出可行域;
易错点
不能准确画出可行域、忽略参数的取值范围导致丢分。
正确答案
(Ⅱ)生产甲种肥料


解析
试题分析:本题属于线性规划的实际应用问题,主要考察了用二元线性规划的基础知识和基本方法解决简单实际问题的能力,以及概括能力和运算求解能力,属于简单题,解线性规划应用问题的一般步骤是:(1)分析题意,设出未知量;(2)列出线性约束条件和目标函数;(3)作出可行域并利用数形结合求解;(4)作答.而求线性规划最值问题,首先明确可行域对应的是封闭区域还是开放区域、分界线是实线还是虚线,其次确定目标函数的几何意义,是求直线的截距、两点间距离的平方、直线的斜率、还是点到直线的距离等等,最后结合图形确定目标函数最值取法.本题只要画对可行域,明确目标函数的意义即可解决,解析如下:
(Ⅱ)解:设利润为z万元,则目标函数







考查方向
解题思路
(Ⅱ)目标函数
易错点
不能准确画出可行域、忽略参数的取值范围导致丢分。
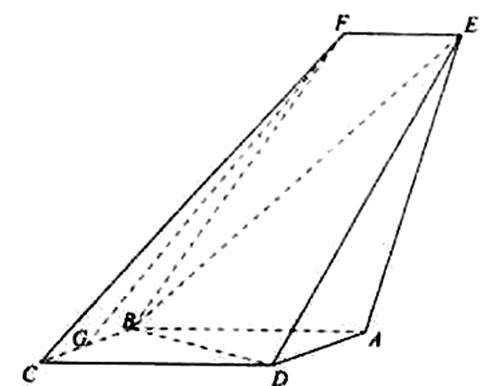
如图,四边形ABCD是平行四边形,平面AED⊥平面ABCD,EF||AB,AB=2,BC=EF=1,AE=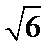
19.求证: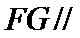
20.求证:平面BED⊥平面AED;
21.求直线EF与平面BED所成角的正弦值.
正确答案
(Ⅰ)证明:取
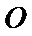
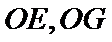
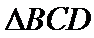
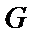

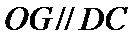
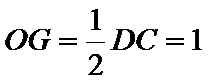
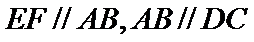

,即四边形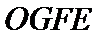
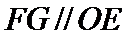
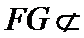

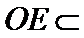
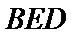
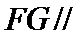
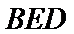
解析
试题分析:本题属于立体几何的综合应用问题,属于中档题,只要掌握相关立体几何的定理及性质,即可解决本题,解析如下:
试题解析:(Ⅰ)证明:取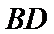
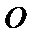


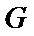


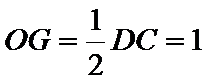
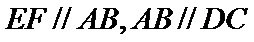

,即四边形
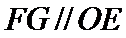



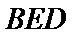
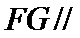

考查方向
解题思路
(Ⅰ)证明线面平行,一般利用线面平行判定定理,即从线线平行出发
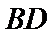

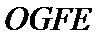
易错点
解题步骤不完整或考虑不全致推理片面导致出错。
正确答案
(Ⅱ)证明:在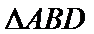
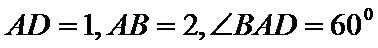
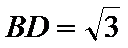
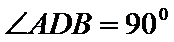

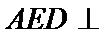
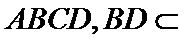
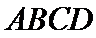
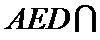
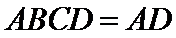
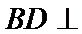
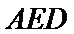
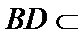
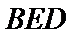
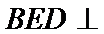
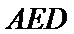
解析
试题分析:本题属于立体几何的综合应用问题,属于中档题,只要掌握相关立体几何的定理及性质,即可解决本题,解析如下:
(Ⅱ)证明:在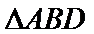
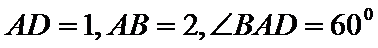

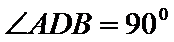
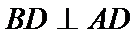
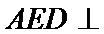


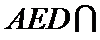
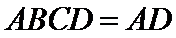
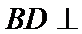
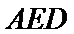
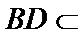

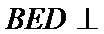

考查方向
解题思路
(Ⅱ)面面垂直的证明,一般转化为证线面垂直,而线面垂直的证明,往往需多次利用线面垂直判定与性质定理,而线线垂直的证明有时需要利用平几条件,如本题可由余弦定理解出
易错点
解题步骤不完整或考虑不全致推理片面导致出错。
正确答案
(Ⅲ)
解析
试题分析:本题属于立体几何的综合应用问题,属于中档题,只要掌握相关立体几何的定理及性质,即可解决本题,解析如下:
(Ⅲ)解:因为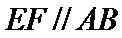
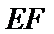

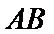
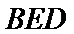
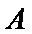
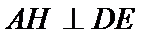

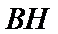


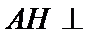
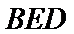
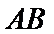




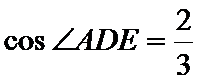


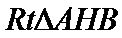
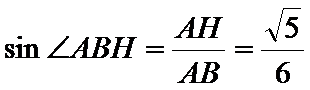
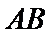

考查方向
解题思路
(Ⅲ)求线面角,关键作出射影,即面的垂线,可利用面面垂直的性质定理得到线面垂直,即面的垂线:过点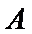

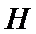
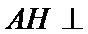


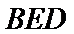
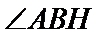
易错点
解题步骤不完整或考虑不全致推理片面导致出错。
设函数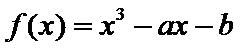
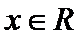
26.求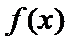
27.若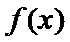
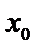
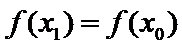
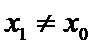
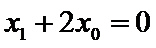
28.设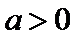
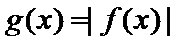
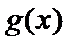
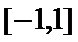
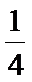
正确答案
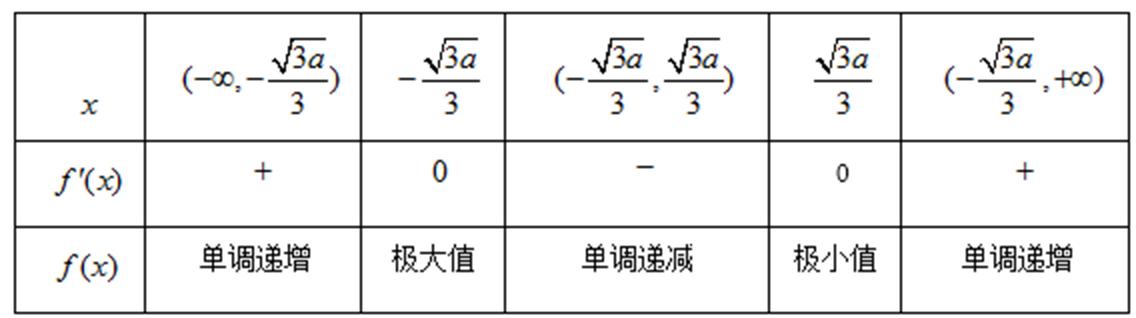
(Ⅰ)递减区间为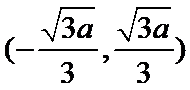
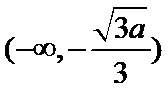
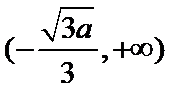
解析
本题主要考察了导数的运算,利用导数研究函数的性质、证明不等式等知识点,属于拔高题,不容易得分,解析如下:
试题解析:(1)解:由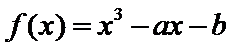
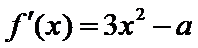
①当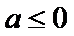
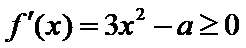
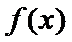
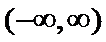
②当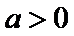
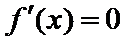
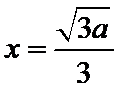
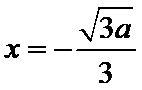
当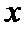
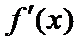
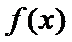
所以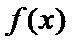
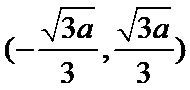
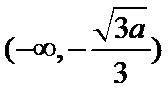
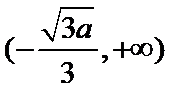
考查方向
解题思路
(Ⅰ)先求函数的导数: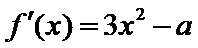
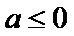
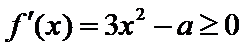
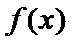
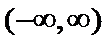
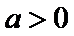
易错点
第二问不知如何就参数的范围进行讨论导致失分。
正确答案
(Ⅱ)证明:因为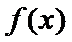
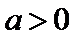
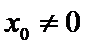
由题意得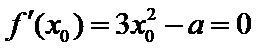
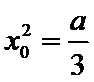
进而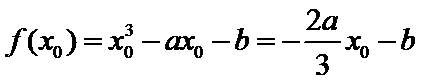
又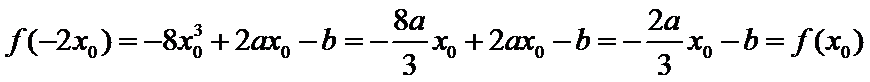
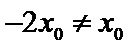
由题意及(1)知,存在唯一实数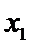
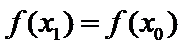
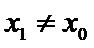
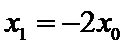
所以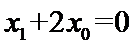
解析
本题主要考察了导数的运算,利用导数研究函数的性质、证明不等式等知识点,属于拔高题,不容易得分.
考查方向
解题思路
(Ⅱ)由题意得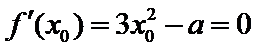
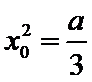
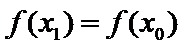
易错点
第二问不知如何就参数的范围进行讨论导致失分。
正确答案
(3)证明:设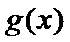
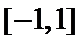
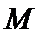
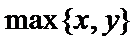
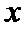
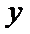
①当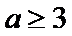
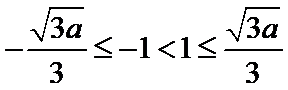
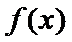
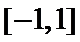
所以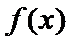
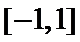
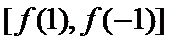
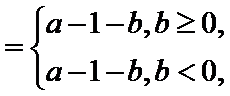
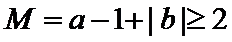
②当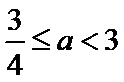
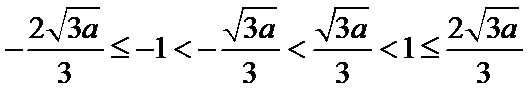
由(1)和(2) 知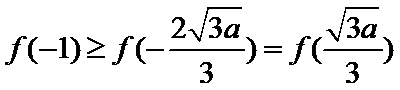
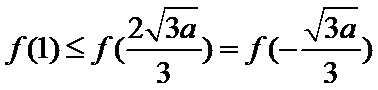
所以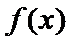
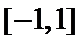
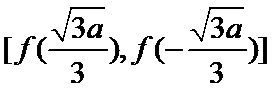
所以
③当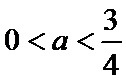
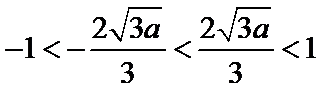
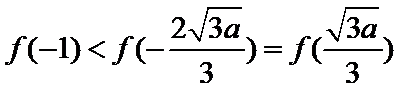
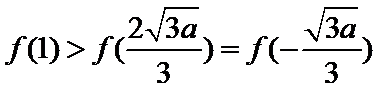
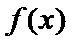
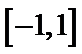
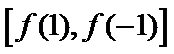
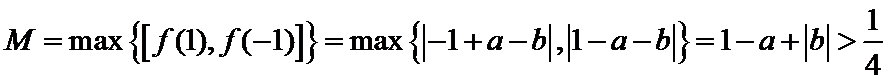
综上所述,当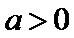
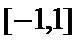
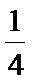
解析
本题主要考察了导数的运算,利用导数研究函数的性质、证明不等式等知识点,属于拔高题,不容易得分.
考查方向
解题思路
(Ⅲ)实质研究函数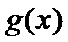
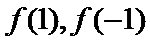
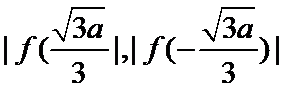
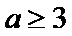
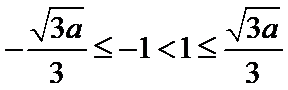
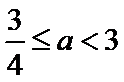
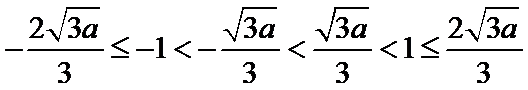
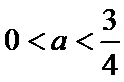
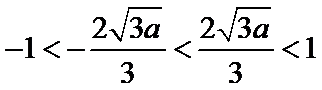
易错点
第二问不知如何就参数的范围进行讨论导致失分。
已知


22.求
23.若对任意的



正确答案
(Ⅰ)
解析
试题分析:本题属于数列的性质及数列求和的综合应用问题,属于简单题,分组转化法求和的常见类型(1)若an=bn±cn,且{bn},{cn}为等差或等比
(2)通项公式为an=的数列,其中
试题解析:(Ⅰ)解:设数列








考查方向
解题思路
(1)根据已知条件
易错点
相关知识点不熟容易处错。
正确答案
(Ⅱ)
解析
试题分析:本题属于数列的性质及数列求和的综合应用问题,属于简单题,分组转化法求和的常见类型(1)若an=bn±cn,且{bn},{cn}为等差或等比
(2)通项公式为an=的数列,其中
(Ⅱ)解:由题意得



设数列


考查方向
解题思路
(2)先根据等差中项的概念求出数列
易错点
相关知识点不熟容易处错。
设椭圆






24.求椭圆的方程;
25.设过点












正确答案
(Ⅰ)
解析
本题主要考察了椭圆的方程、直线与椭圆的位置关系等知识点,属于拔高题,不容易得分。解决直线与椭圆的位置关系的相关问题,其常规思路是先把直线方程与椭圆方程联立,消元、化简,然后应用根与系数的关系建立方程,解决相关问题.直线与圆锥曲线位置关系的判断、有关圆锥曲线弦的问题等能很好地渗透对函数方程思想和数形结合思想的考查,一直是高考考查的重点,特别是焦点弦和中点弦等问题,涉及中点公式、根与系数的关系以及设而不求、整体代入的技巧和方法,也是考查数学思想方法的热点题型.本题只有熟练掌握相关知识点,并能够灵活运用这些知识点,才能够得分,具体解体过程如下:
试题解析:(1)解:设







考查方向
解题思路
(Ⅰ)求椭圆标准方程,只需确定量,由



易错点
第二问不知如何处理已知条件导致本题没思路。
正确答案
(Ⅱ)
解析
本题主要考察了椭圆的方程、直线与椭圆的位置关系等知识点,属于拔高题,不容易得分。解决直线与椭圆的位置关系的相关问题,其常规思路是先把直线方程与椭圆方程联立,消元、化简,然后应用根与系数的关系建立方程,解决相关问题.直线与圆锥曲线位置关系的判断、有关圆锥曲线弦的问题等能很好地渗透对函数方程思想和数形结合思想的考查,一直是高考考查的重点,特别是焦点弦和中点弦等问题,涉及中点公式、根与系数的关系以及设而不求、整体代入的技巧和方法,也是考查数学思想方法的热点题型.本题只有熟练掌握相关知识点,并能够灵活运用这些知识点,才能够得分,具体解体过程如下:
(2)设直线的斜率为


设


整理得


由题意得

由(1)知



由









即

解得

所以直线


考查方向
解题思路
(Ⅱ)先化简条件:



易错点
第二问不知如何处理已知条件导致本题没思路。