- 真题试卷
- 模拟试卷
- 预测试卷
2. “a=0”是“直线l1：x+ay﹣a=0与l2：ax﹣（2a﹣3）y﹣1=0”垂直的（ ）
正确答案
解析
若两直线垂直，则a﹣a（2a﹣3）=0，即a（4﹣2a）=0，
解得a=0或a=2，
故“a=0”是“直线l1：x+ay﹣a=0与l2：ax﹣（2a﹣3）y﹣1=0”垂直充分不必要条件，
故选：B
知识点
3.某锥体三视图如下，根据图中所标数据，该锥体的各侧面中，面积最大的是（ ）
A3
B2
C6
D8
正确答案
解析
因为三视图复原的几何体是四棱锥，顶点在底面的射影是底面矩形的长边的中点，底面边长分别为4，2，后面是等腰三角形，腰为3，所以后面的三角形的高为：
知识点
4.将函数y=sin（2x﹣
Ay=sin（x﹣
By=sin（x﹣
Cy=sin4x
Dy=sinx
正确答案
解析
将函数y=sin（2x﹣
知识点
5.过原点且倾斜角为60°的直线被圆x2+y2﹣4y=0所截得的弦长为（ ）
A
B2
C
D
正确答案
解析
将圆x2+y2﹣4y=0的方程可以转化为：
x2+（y﹣2）2=4，
即圆的圆心为A（0，2），半径为R=2，
∴A到直线ON的距离，即弦心距为1，
∴ON=
∴弦长2
故选D.
知识点
6.设
A若
B若
C若
D若
正确答案
解析
由直线与平面的性质可知当
知识点
1.设集合
正确答案
解析
根据题意，集合A={0，2，a}，B={1，a2}，
且A∪B={0，1,2，4，16}，则有a=4，故选：D.
知识点
10.一艘海轮从A处出发，以每小时40海里的速度沿东偏南50°方向直线航行，30分钟后到达B处.在C处有一座灯塔，海轮在A处观察灯塔，其方向是东偏南20°，在B处观察灯塔，其方向是北偏东65°，那么B、C两点间的距离是（ ）
A
B
C
D
正确答案
解析
略
知识点
8.函数f（x）=ln（x2+1）的图象大致是（ ）
A
B
C
D
正确答案
解析
∵x2+1≥1，又y=lnx在（0，+∞）单调递增，∴y=ln（x2+1）≥ln1=0，
∴函数的图象应在x轴的上方，又f（0）=ln（0+1）=ln1=0，∴图象过原点，
综上只有A符合．
故选：A
知识点
9.称
A
B
C
D
正确答案
解析
如图：
∵|
用
∴d（
|
知识点
7.函数f（x）=x+sinx（x∈R）（ ）
正确答案
解析
∵f（x）=x+sinx，
∴f（﹣x）=﹣x﹣sinx=﹣f（x），则函数f（x）是奇函数．
函数的导数f′（x）=1+cosx≥0，
则函数f（x）单调递增，为增函数．
故选：D.
知识点
12.在约束条件
正确答案
7
解析
作出不等式组对于的平面区域如图：
由z=3x+2y，则y=
平移直线y=
经过点B时，直线y=
由
此时zmin=3×1+2×2=7，
故答案为：7
知识点
14.在长为12cm的线段AB上任取一点C，现作一矩形，使邻边长分别等于线段AC、CB的长，则该矩形面积大于20cm2的概率为 ．
正确答案
解析
设AC=x，则BC=12﹣x
矩形的面积S=x（12﹣x）＞20
∴x2﹣12x+20＜0
∴2＜x＜10
由几何概率的求解公式可得，矩形面积大于20cm2的概率P=
故答案为：
知识点
13.阅读如图所示的程序框图，运行相应的程序，输出的S值为 ；
正确答案
0
解析
模拟执行程序，可得
S=1，i=1
S=3，i=2，不满足条件i＞4，S=4，i=3
不满足条件i＞4，S=1，i=4
不满足条件i＞4，S=0，i=5
满足条件i＞4，退出循环，输出S的值为0．
故答案为：0．
知识点
15.若函数
正确答案
2
解析
略
知识点
16.已知向量
正确答案
8
解析
∵
∴4（x﹣1）+2y=0即4x+2y=4
∵
当且仅当24x=22y即4x=2y=2取等号
故答案为8
知识点
17.若直线
正确答案
解析
当
当
知识点
11.已知复数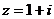
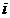
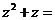
正确答案
解析
由z=1+i，得z2+z=（1+i）2+（1+i）=1+2i+i2+1+i=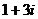
故答案为：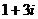
知识点
20.如图所示，在三棱锥
（1）求证：
（2）求直线
正确答案
见解析。
解析
（1）过
又
（2）解法1：
则
解法2：设直线
又
知识点
21. 已知函数f（x）=2lnx+
（1）当函数f（x）在点（1，f（1））处的切线与直线y﹣4x+1=0垂直时，求实数m的值；
（2）若x≥1时，f（x）≥1恒成立，求实数m的取值范围．
正确答案
（1）9
（2） [2，+∞）
解析
（1）∵f′（x）=
∴函数f（x）在点（1，f（1））处的切线的斜率k=f′（1）=2﹣
∵函数f（x）在点（1，f（1））处的切线与直线y﹣4x+1=0垂直，
∴2﹣
∴m=9；
（2）依题意不等式2lnx+
∴x≥1时，g′（x）＜0，∴函数g（x）在[1，+∞）时为减函数，∴g（x）≤g（1）=2，∴m≥2
即实数m的取值范围是[2，+∞）．
知识点
18. 在锐角
（1）求角
（2）若函数
正确答案
（1）
（2）
解析
（1）由
化为2sinBcosA=sin（C+A）=sinB，∵sinB≠0，∴cosA=
∵A∈
（2）y=
∵B+C=
∴
知识点
22.设抛物线C：
（1）求抛物线C的方程;
（2）设点F是抛物线C的焦点，N为抛物线C上的一动点，过N作抛物线C的切线交圆O于P、Q两点，求
正确答案
（1）
解析
（1）因为抛物线C的准线方程为
（2）设N（
因为圆心O到直线PQ的距离为
设点F到直线PQ的距离为d，则
所以，
当
知识点
19.已知公差为d的等差数列{an}满足：an+an+1=2n，n∈N*．
（1）求首项a1和公差d，并求数列{an}的通项公式；
（2）令
正确答案
见解析。
解析
（1）∵公差为d的等差数列{an}满足：an+an+1=2n，n∈N*．
令n=1，2，可得a1+a2=2，a2+a3=4，
∴2d=2，解得d=1，
∴2a1+d=2，解得a1=
∴
（2）∵an+an+1=2n，n∈N*．
∴
∴数列{bn}的前n项和Sn=b1+b2+…+bn=
