- 真题试卷
- 模拟试卷
- 预测试卷
1.方程

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.若一个圆锥的侧面积是底面积的3倍,则圆锥的母线与轴的夹角的大小为__________ (用反三角形式表示)
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.已知

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.已知将函数




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2.不等式


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.已知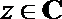

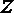
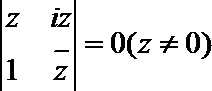
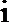
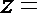
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.有5本不同的书,其中语文书2本,数学书2本,物理书1本。若将其随机地并排摆放到书架的同一层上,则同一科目的书都相邻的概率为__________
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.若对任意实数


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.如图所示是毕达哥拉斯的生长程序:正方形上连接着一个等腰直角三角形,等腰直角三角形的直角边上再连接正方形

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12.求函数
正确答案
3
解析
解析已在路上飞奔,马上就到!
知识点
13.已知


正确答案
5
解析
解析已在路上飞奔,马上就到!
知识点
14.已知公差为








正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.设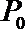
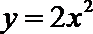
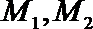
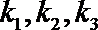
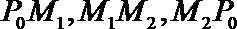
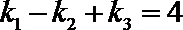
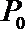
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
24.在谈到某些图书的价格时,有人认为:“每一份的品质都是由每一份的成本堆积起来的,没有真正物美价廉的东西。”这一观点蕴含的经济道理是( )
正确答案
解析
解析已在路上飞奔,马上就到!
16.某学校高三年级共有学生200人,其中男生120人,女生80人.为了调查学生的学习状况,用分层抽样的方法从该校高三全体学生中抽取一个容量为25的样本,则应抽取女生的人数为( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15.已知数列


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17.函数

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18.已知




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19.已知正方体



(1)求异面直线

(2)求四面体
正确答案
(1)由



连接


所以
即异面直线


(利用空间向量同样给分)
(2)算出




该四面体

解析
解析已在路上飞奔,马上就到!
知识点
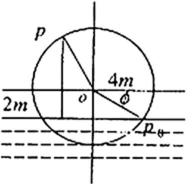
20.如图,一个水轮的半径为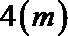
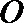
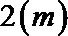
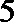

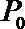
(1)将点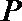
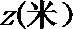
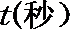
(2)求点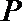
正确答案
(1)如图建立直角坐标系,设角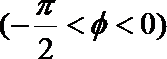
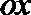
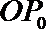
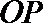
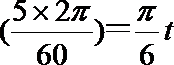
得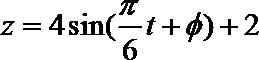
当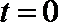
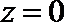
得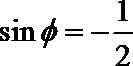
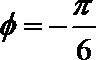
故所求的函数关系式为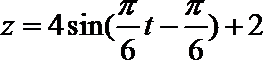
(2)令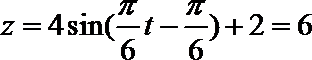
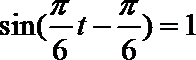
取
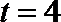
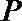
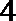
解析
解析已在路上飞奔,马上就到!
知识点
22.如图已知椭圆






(1)求椭圆
(2)已知垂直于








(3)在






正确答案
(1)由题设得
解得: 
故

(2)证明:

直线

①×②,得

代入③得

因为点


即点

(3)设直线
结合第(2)问的结论

所以
解析
解析已在路上飞奔,马上就到!
知识点
23.将各项均为正数的数列




已知数列



(1)求数阵中第




(2)试问
(3)试问这个数列中是否有
正确答案
(1)由已知可得:
解得:
(2)由

知


(3)假设


由第


知
当

当
于是,不等式整数解。
从而,
解析
解析已在路上飞奔,马上就到!
知识点
21.已知





(1)若


(2)设





正确答案
(1)“







(2) 当
对任意






由


解析
解析已在路上飞奔,马上就到!