- 真题试卷
- 模拟试卷
- 预测试卷
1.若集合A={x|x>0},B={x|x<3},则A∩B等于( )
正确答案
解析
根据题意,在数轴上表示出A、B,可得:进而由交集的定义,取两个集合的公共部分,可得A∩B={x|0<x<3},故选B。
知识点
2.i是虚数单位,
正确答案
解析


知识点
5.函数
正确答案
解析
本题考查的是对数函数的图象,由函数解析式可知

知识点
9.执行如图所示的程序框图,若输入的x,t均为2,则输出的S=( )
正确答案
解析
若x=t=2,则第一次循环,1≤2成立,则M=

知识点
6.已知向量a=(x-1,2),b=(2,1),则a⊥b的充要条件是()
正确答案
解析
有向量垂直的充要条件得2(x-1)+2=0 所以x=0 , 选D。
知识点
8.若变量


正确答案
解析
本题考查的简单线性规划,如图,可知目标函数最大值和最小值分别为4和2。
故选B.
知识点
10.设函数f(x),g(x)的定义域都为R,且f(x)是奇函数,g(x)是偶函数,则下列结论中正确的是( )
正确答案
解析
f(x)是奇函数,g(x)是偶函数,∴|f(x)|为偶函数,|g(x)|为偶函数。
再根据两个奇函数的积是偶函数、两个偶函数的积还是偶函数、一个奇函数与一个偶函数的积是奇函数,可得 f(x)|g(x)|为奇函数,故选C。
知识点
3.一个几何体的三视图形状都相同,大小均等,那么这个几何体不可以是()
正确答案
解析
分别比较A、B、C的三视图不符合条件,D 符合。
知识点
4.若tanα>0,则( )
正确答案
解析
∵tanα>0,∴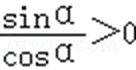
知识点
7.已知双曲线

正确答案
解析
双曲线

知识点
12.在整数集Z中,被5除所得余数为k的所有整数组成一个“类”,记为[k],即[k]={5n+k丨n∈Z},k=0,1,2,3,4。给出如下四个结论:
①2011∈[1]
②-3∈[3];
③Z=[0]∪[1]∪[2]∪[3]∪[4]
④“整数a,b属于同一‘类’”的充要条件是“a-b∈[0]”。
其中,正确结论的个数是()
正确答案
解析
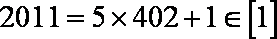
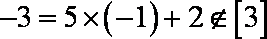
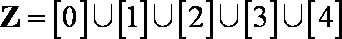
若整数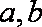
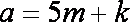
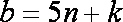
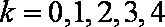
则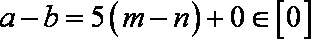
由以上,①,③,④正确,故选C。
知识点
11.设x,y满足约束条件,则z=x+2y的最大值为( )
正确答案
解析
作出不等式对应的平面区域,由z=x+2y,得y=﹣



由

故选B.
知识点
19.如图,在长方体ABCD-A1B1C1D1中,AB=AD=1,AA1=2,M为棱DD1上的一点。
(1)求三棱锥A-MCC1的体积;
(2)当A1M+MC取得最小值时,求证:B1M⊥平面MAC
正确答案
见解析。
解析
(1)又长方体AD


∴


(2)将侧面











∴




∵


∴CM⊥平面


知识点
18.如图,在等腰直角三角形




(1)若

(2)若点




正确答案
见解析。
解析
(1)在



由余弦定理得,
得
解得

(2)设

在

所以
同理
故
因为








知识点
21.设F1,F2分别是C:

(1)若直线MN的斜率为
(2)若直线MN在y轴上的截距为2,且|MN|=5|F1N|,求a,b。
正确答案
见解析。
解析
(1)∵M是C上一点且MF2与x轴垂直,∴M的横坐标为c,当x=c时,y=

若直线MN的斜率为



则

(2)由题意,原点O是F1F2的中点,则直线MF1与y轴的交点D(0,2)是线段MF1的中点,故
由|MN|=5|F1N|,解得|DF1|=2|F1N|,设N(x1,y1),由题意知y1<0,
则


将b2=4a代入得
知识点
20.袋中有大小、形状相同的红、黑球各一个,现一次有放回地随机摸取3次,每次摸取一个球
(1)试问:一共有多少种不同的结果?请列出所有可能的结果;
(2)若摸到红球时得2分,摸到黑球时得1分,求3次摸球所得总分为5的概率。
正确答案
见解析。
解析
(1)一共有8种不同的结果,列举如下:
(红、红、红、)、(红、红、黑)、(红、黑、红)、(红、黑、黑)、(黑、红、红)、(黑、红、黑)、
(黑、黑、红)、(黑、黑、黑)
(2)本题是一个等可能事件的概率
记“3次摸球所得总分为5”为事件A
事件A包含的基本事件为:(红、红、黑)、(红、黑、红)、(黑、红、红)事件A包含的基本事件数为3
由(I)可知,基本事件总数为8,
∴事件A的概率为
知识点
17.数列{an}中,a1=

(1)求数列{an}的通项公式an以及前n项和Sn;
(2)若S1,t(S1+S2),3(S2+S3)成等差数列,求实数t的值。
正确答案
见解析。
解析
(1)由Sn+1﹣Sn=(

又

从而
(2)由(Ⅰ)可得


从而由S1,t(S1+S2),3(S2+S3)成等差数列可得:
知识点
22.已知a,b为常数,且a≠0,函数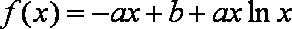
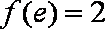
(1)求实数b的值;
(2)求函数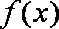
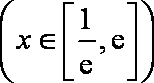
(3)当a=1时,是否同时存在实数m和M(m<M),使得对每一个t∈[m,M],直线y=t与曲线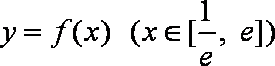
正确答案
见解析。
解析
(1)由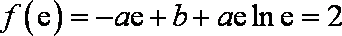
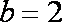
(2)由(Ⅰ),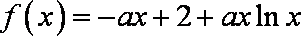

从而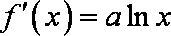
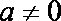
(1) 当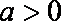
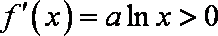
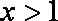
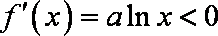
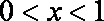
(2) 当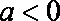
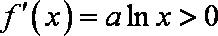
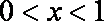
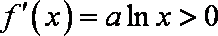
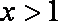
因而, 当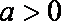
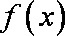
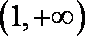
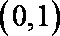
当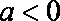
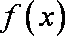
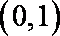
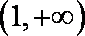
(3)当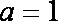
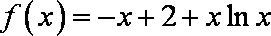
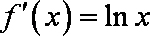
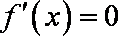
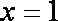
当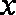


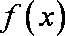
因为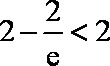
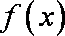

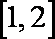
由此可得,
若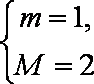

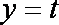
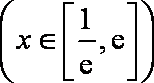
并且对每一个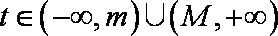
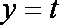
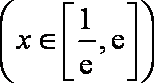
综合以上,当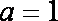
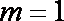

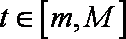
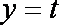
知识点
13.将容量为n的样本中的数据分成6组,绘制频率分布直方图,若第一组至第六组数据的频率之比为2:3:4:6:4:1,且前三组数据的频数之和等于27,则n等于()
正确答案
60
解析
设第一组至第六组数据的频率分别为2x,3x,4x,6x,4x,x,则2x+3x+4x+6x+4x+x=1,解得


故答案为60。
知识点
16.五位同学围成一圈依序循环报数,规定:①第一位同学首次报出的数为1,第二位同学首次报出的数也为1,之后每位同学所报出的数都是前两位同学所报出的数之和;②若报出的是3的倍数,则报该数的同学需拍手一次,当第30个数被报出时,五位同学拍手的总次数为 _________ 。
正确答案
7
解析
这个数列的变化规律是:从第三个数开始递增,且是前两项之和,那么有1、1、2、3、5、8、13、21、34、55、89、144、233、377、610、987
分别除以3得余数分别是1、1、2、0、2、2、1、0、1、1、2、0、2、2、1、0
由此可见余数的变化规律是按1、1、2、0、2、2、1、0
循环周期是8。
在这一个周期内第四个数和第八个数都是3的倍数,
所以在三个周期内共有6个报出的数是三的倍数,
后面6个报出的数中余数是1、1、2、0、2、2,只有一个是3的倍数,故3的倍数总共有7个,
也就是说拍手的总次数为7次。
故答案为:7。
知识点
14.若△ABC的面积为

正确答案
2
解析






知识点
15.已知函数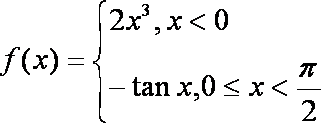

正确答案
-2
解析