- 真题试卷
- 模拟试卷
- 预测试卷
5.执行如图所示的程序框图,输出的
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.在棱长为1的正方体



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2.在等比数列



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.已知向量



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.过双曲线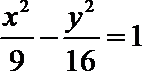
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.若满足条件


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.已知函数



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
1.已知集合


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.复数
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.若

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.以抛物线

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12.已知三条侧棱两两垂直的正三棱锥的俯视图如图所示,那么此三棱锥的体积是( ),左视图的面积是( ).
正确答案

解析
解析已在路上飞奔,马上就到!
知识点
13.设某商品的需求函数为






正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14.已知函数

下面三个命题中,所有真命题的序号是 ( ).
① 函数
② 任取一个不为零的有理数


③ 存在三个点

正确答案
1 ; ①②③
解析
解析已在路上飞奔,马上就到!
知识点
15.已知函数
(1)求
(2)在







正确答案
(1)


由
得:
所以 


(2)因为 
所以 

因为 

所以 
因为 

所以 
因为 



所以 

解析
解析已在路上飞奔,马上就到!
知识点
16.某学校随机抽取部分新生调查其上学所需时间(单位:分钟),并将所得数据绘制成频






(1)求直方图中
(2)如果上学所需时间不少于1小时的学生可申请在学校住宿,请估计学校600名新生中有多少名学生可以申请住宿.
正确答案
(1)由直方图可得

所以
(2)由直方图可知,新生上学所需时间不少于1小时的频率为:
因为 
所以 600名新生中有72名学生可以申请住宿.
解析
解析已在路上飞奔,马上就到!
知识点
18.已知函数
(Ⅰ)求
(Ⅱ)是否存在实数



正确答案
(Ⅰ)


当


所以 
当



函数


所以 


综上所述,当


当




(Ⅱ)由(Ⅰ)可知:
当



所以




当
① 当



所以




② 当



所以 
又 
所以 


综上所述,存在实数


解析
解析已在路上飞奔,马上就到!
知识点
17.已知菱形ABCD中,AB=4, 



(Ⅰ)证明:BD //平面
(Ⅱ)证明:
(Ⅲ)当
正确答案
证明:(Ⅰ)因为点

所以
又



所以

(Ⅱ)
在菱形


则
所以 在三棱锥

又
所以 

又 

所以 
(Ⅲ)
连结


所以 
所以 
因为 


又 

所以 



又 

所以 
因为 

所以 
解析
解析已在路上飞奔,马上就到!
知识点
19.已知椭圆



(Ⅰ)求椭圆
(Ⅱ)已知








正确答案
解:(Ⅰ)因为 


又 

所以 
所以 椭圆

(Ⅱ)当直线




所以 
当直线
设直线


则直线DE的方程为
由 

即
所以
所以 
所以 
即 
类似可求
所以
设


令

所以 
所以 
综上,

解析
解析已在路上飞奔,马上就到!
知识点
20.对于集合M,定义函数

(Ⅰ)写出


(Ⅱ)用Card(M)表示有限集合M所含元素的个数.
(ⅰ)求证:当

(ⅱ)求
正确答案
(Ⅰ)解:

(Ⅱ)设当

(ⅰ)证明:假设

那么

所以 

(ⅱ)同(ⅰ)可得:

若存在


那么

所以 集合

若




综上可知,当


解析
解析已在路上飞奔,马上就到!