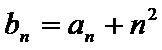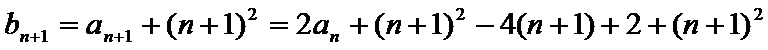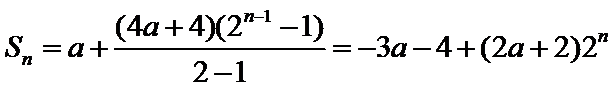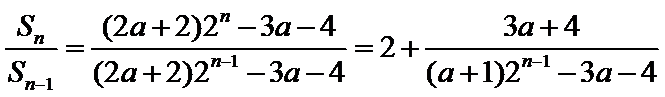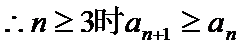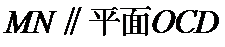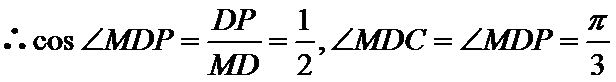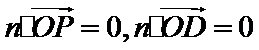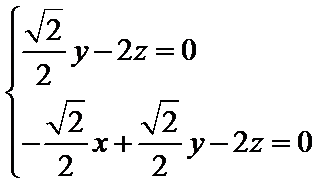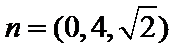- 真题试卷
- 模拟试卷
- 预测试卷
1. 设


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.把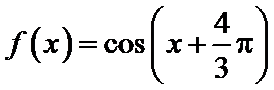
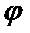
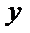
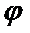
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.不等式
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.若函数

正确答案
2
解析
解析已在路上飞奔,马上就到!
知识点
2.
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.如果


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.如图,在平行四边形




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.已知命题“任意


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12.已知函数






①
②
③
④
其中,不可能成立的结论的序号是( )
正确答案
④
解析
解析已在路上飞奔,马上就到!
知识点
10.若直线


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14.设函数




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
13.已知函数

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.若函数




正确答案
10
解析
解析已在路上飞奔,马上就到!
知识点
3.在二项式

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18.设


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.在空间四边形











正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15.从






正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17.已知



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
22.已知焦点在





(1)求椭圆
(2)已知过点




(3)若直线


正确答案
(1)设椭圆

且
由题意可知:

所以
所以,椭圆
(2)由(1)得
当直线


由
解得:

即


则直线
直线
因为
所以
所以
解析
解析已在路上飞奔,马上就到!
知识点
19.已知函数


(1)试确定
(2)若不等式


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
20.在


(1)求
(2)若

正确答案
(1)因为
所以
又
=

(2)由已知得
因为
所以
又因为
所以
当且仅当

此时
所以
解析
解析已在路上飞奔,马上就到!
知识点
23.已知数列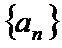
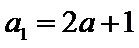
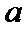
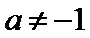
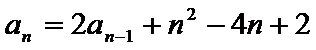
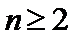
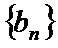
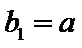
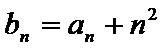
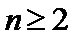
(1)证明: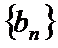
(2)设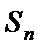
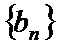
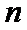
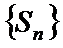
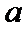
(3)当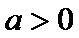
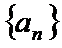
正确答案
(1)∵
∴
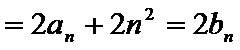
由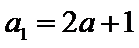
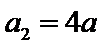
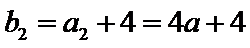
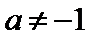
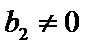
即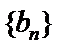
(2)
当n≥2时,
∵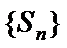
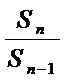
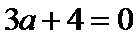
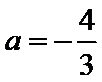
(3)由(1)知当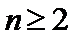
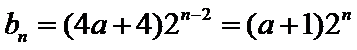
所以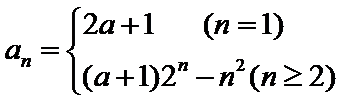
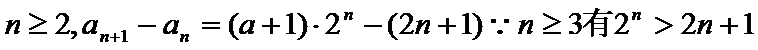
显然最小项是前三项中的一项.
当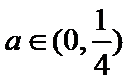
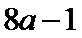
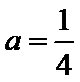
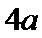
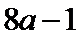
当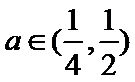
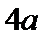
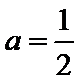
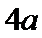
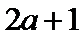
当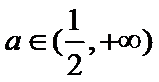
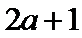
解析
解析已在路上飞奔,马上就到!
知识点
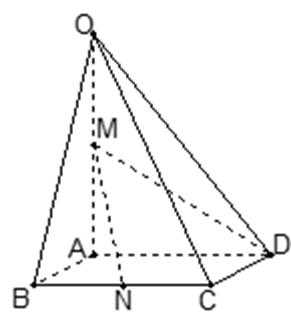
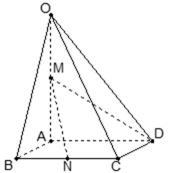
21.如图,在四棱锥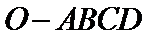
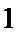
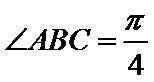
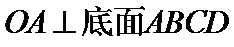
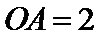
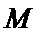

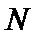
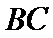
(1)证明:直线
(2)求异面直线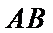
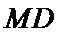
正确答案
方法一(综合法)
(1)取OB中点E,连接ME,NE
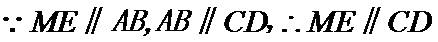
又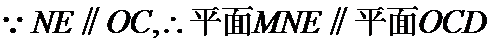
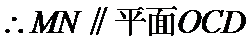
(2)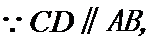
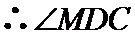
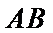
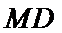


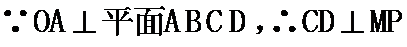
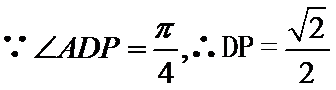
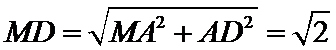
所以 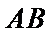
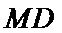
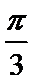
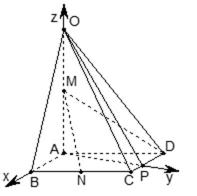
方法二(向量法)作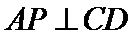
如图,分别以AB,AP,AO所在直线为
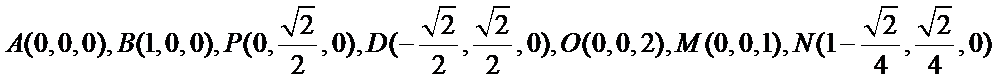
(1)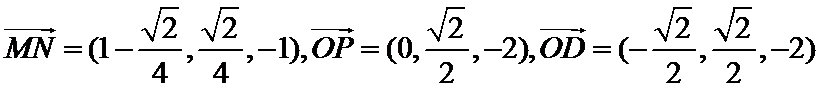
设平面OCD的法向量为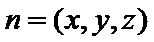
则
即
取
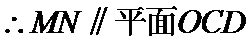
(2)设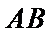
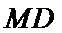

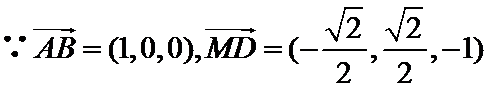
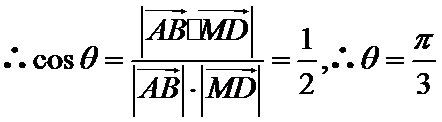
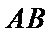
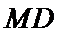
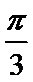
解析
解析已在路上飞奔,马上就到!