文科数学 2015年高三试卷

精品

单选题
填空题
简答题

立即下载

文科数学热门试卷

X 查看更多试卷

试卷目录

1、单选题

2、填空题

3、简答题

真题试卷
模拟试卷
预测试卷

单选题本大题共10小题，每小题5分，共50分。在每小题给出的4个选项中，有且只有一项是符合题目要求。

题型：单选题

分值: 5分

2．已知集合，，则等于（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

集合的含义

题型：单选题

分值: 5分

4．在区间上随机取一个实数，使得的概率为（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

任意角的概念

题型：单选题

分值: 5分

5．将函数的图象向右平移个单位，得到的图象关于原点对称，则的最小正值为（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

函数的概念及其构成要素

题型：单选题

分值: 5分

6．已知某几何体的三视图，则该几何体的体积是（）

A12

B24

C36

D48

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

空间几何体的结构特征

题型：单选题

分值: 5分

7．直线与不等式组表示的平面区域有公共点，则实数的取值范围是（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

不等式的性质

题型：单选题

分值: 5分

10．对于函数，若存在实数，使得的解集为，则实数的取值范围是（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

函数的概念及其构成要素

题型：单选题

分值: 5分

1．设是虚数单位，则复数等于（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

虚数单位i及其性质

题型：单选题

分值: 5分

3．“”是“函数为实数集上的奇函数”的（）

A充分不必要条件

B必要不充分条件

C充要条件

D既不充分又不必要条件

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

函数的概念及其构成要素

题型：单选题

分值: 5分

8．已知圆心为，半径为1的圆上有不同的三个点，其中，存在实数满足，则实数的关系为（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

函数的概念及其构成要素

题型：单选题

分值: 5分

9．已知抛物线的准线与双曲线相交于A、B两点，双曲线的一条渐近线方程是，点F是抛物线的焦点，且△FAB是等边三角形，则该双曲线的标准方程是（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

函数的概念及其构成要素

填空题本大题共5小题，每小题5分，共25分。把答案填写在题中横线上。

题型：填空题

分值: 5分

11．为了解某校教师使用多媒体辅助教学的情况，采用简单随机抽样的方法，从该校200名授课教师中抽取20名教师，调查了解他们上学期使用多媒体辅助教学的次数，结果用茎叶图表示（如图），据此可估计该校上学期200名教师中，使用多媒体辅助教学不少于30次的教师人数为________________。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

函数的概念及其构成要素

题型：填空题

分值: 5分

13．等差数列中，，则________________。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

由数列的前几项求通项

题型：填空题

分值: 5分

14．已知为正实数，直线与圆相切，则的取值范围是________________。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

直线的倾斜角与斜率

题型：填空题

分值: 5分

15．对于函数，给出下列结论：

①等式时恒成立；

②函数的值域为；

③函数在R上有三个零点；

④若；

⑤若；

其中所有正确结论的序号为________________。

正确答案

①②④

解析

解析已在路上飞奔，马上就到！

知识点

四种命题及真假判断

题型：填空题

分值: 5分

12．执行如图所示的程序，则输出的结果为________________。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

程序框图

简答题（综合题）本大题共75分。简答应写出文字说明、证明过程或演算步骤。

题型：简答题

分值: 12分

17.是指空气中直径小于或等于微米的颗粒物（也称可入肺颗粒物）．为了探究车流量与的浓度是否相关，现采集到某城市周一至周五某一时间段车流量与的数据如下表：

（Ⅰ）根据上表数据，用最小二乘法求出关于的线性回归方程；

（Ⅱ）若周六同一时间段车流量是万辆，试根据（Ⅰ）求出的线性回归方程预测，此时的浓度为多少（保留整数）？

（参考公式：，参考数据：）

正确答案

解：（Ⅰ）由条件可知，

故关于的线性回归方程为；

（Ⅱ）当时，，

所以可以预测此时的浓度约为37．

解析

解析已在路上飞奔，马上就到！

知识点

函数的概念及其构成要素

题型：简答题

分值: 12分

18．已知数列和对任意的满足，若数列是等比数列，且．

（Ⅰ）求数列和的通项公式；

（Ⅱ）设，求数列的前项和．

正确答案

解：（Ⅰ）由条件可知，得，于是，

，解得，

又数列是等比数列，则公比为，于是，

又，于是，

解得．

（Ⅱ）由题意得，

．

解析

解析已在路上飞奔，马上就到！

知识点

函数的概念及其构成要素

题型：简答题

分值: 13分

21．设函数

（Ⅰ）当时，求函数的单调区间；

（Ⅱ）若对任意恒成立，求实数的最小值．

正确答案

解：（Ⅰ）的定义域为

当时，，

当时，，单调递减

当时，，单调递增，

综上，的单调递增区间为，单调递减区间为

（Ⅱ）由题意知：，在上恒成立，

即在区间上恒成立，

又，在区间上恒成立

设，，则

又令，则

当时，，单调递减，，

即在恒成立

所以在单调递增，，

故，所以实数的最小值为．

解析

解析已在路上飞奔，马上就到！

知识点

函数的概念及其构成要素

题型：简答题

分值: 12分

16．在中，角所对的边分别为，，，函数的图象关于直线对称．

（Ⅰ）当时，求函数的最大值并求相应的的值；

（Ⅱ）若且，求的面积．

正确答案

解：．

（Ⅰ）由函数的图像关于直线对称，知

解得

又，所以当时，．

当时，，

于是当，即时，函数的最大值为；

（Ⅱ）由正弦定理得，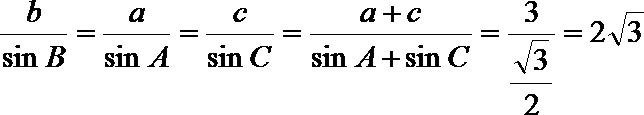

又得，

由余弦定理得，

解得，

于是的面积为．

解析

解析已在路上飞奔，马上就到！

知识点

解三角形的实际应用

题型：简答题

分值: 13分

19.如图，在多面体中，四边形是正方形，是等边三角形，。

（1）求证：；

（2）求多面体的体积。

正确答案

证明及解：

（1）取中点，连，

∥

∥，∥

四边形是平行四边形

∥，∥

又平面，平面

∥平面

在正方形中，∥，∥，

四边形为平行四边形

∥

又平面，平面

∥平面

，平面∥平面

又平面

∥平面．

（2）在正方形中，

又是等边三角形，所以，

所以

于是

又，平面，

又，平面

于是多面体是由直三棱柱和四棱锥组成的．

又直三棱柱的体积为，

四棱锥的体积为，

故多面体的体积为．

解析

解析已在路上飞奔，马上就到！

知识点

空间几何体的结构特征

题型：简答题

分值: 13分

20．在平面直角坐标系xOy中，已知对于任意实数，直线恒过定点F．设椭圆C的中心在原点，一个焦点为F，且椭圆C上的点到F的最大距离为．

（Ⅰ）求椭圆C的方程；

（Ⅱ）设（m，n）是椭圆C上的任意一点，圆O：与椭圆C有4个相异公共点，试判断圆O与直线l1：mx+ny=4的位置关系．

正确答案

解：（Ⅰ）,

解得．

设椭圆C的长轴长、短轴长、焦距分别为2a，2b，2c，

则由题设，知于是a=2，b2=1．

所以椭圆C的方程为

（Ⅱ）因为圆O：与椭圆C有4个相异公共点，

所以，即

因为点（m，n）是椭圆上的点，所以．

所以．

于是圆心O到直线l1的距离

故直线l1与圆O相离．

解析

解析已在路上飞奔，马上就到！

知识点

椭圆的定义及标准方程

文科数学 热门试卷

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

文科数学热门试卷