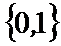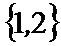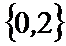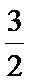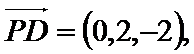- 真题试卷
- 模拟试卷
- 预测试卷
2.函数
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.设数列
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.函数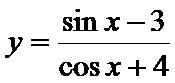
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.到椭圆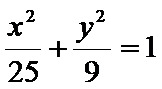
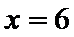
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.三棱锥P-ABC的三条侧棱PA、PB、PC两两互相垂直,且长度分别为3、4、5,则三棱锥P-ABC外接球的表面积是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12. 已知函数


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
1.若集合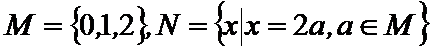
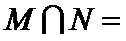
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5. 函数



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.已知双曲线

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.已知函数



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.若
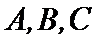
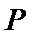
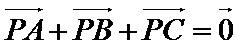
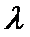
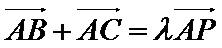
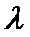
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.在航天员进行的一项太空实验中,先后要实施6个程序,其中程序A只能出现在第一步或最后一步,程序B和C实施时必须相邻,则实验顺序的编排方法共有( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14.
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
13.如果实数


正确答案
1
解析
解析已在路上飞奔,马上就到!
知识点
15.如图,正六边形ABCDEF的两个顶点A、D为椭圆的两个焦点,
其余4个顶点在椭圆上,则该椭圆的离心率是___________。
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.关于正四棱锥
①异面直线
②侧面为锐角三角形;
③侧面与底面所成的二面角大于侧棱与底面所成的角;
④相邻两侧面所成的二面角为钝角;
其中正确的命题序号是___________。
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17.已知数列







正确答案
解:∵数列是等比数列 ∴
由


∴
∴
解析
解析已在路上飞奔,马上就到!
知识点
18.在



(Ⅰ)若


(Ⅱ)若

正确答案
解:
(Ⅰ)由余弦定理及已知条件得,
又因为



联立方程组


(Ⅱ)由题意得
即
当




当


联立方程组


所以

解析
解析已在路上飞奔,马上就到!
知识点
20.如图,在四棱锥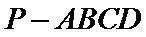


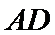

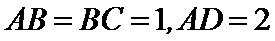
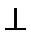


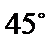

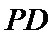
(Ⅰ)求证: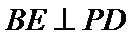
(Ⅱ)求二面角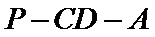
正确答案
解:
解法二:(1) 如图,建立空间直角坐标系,由已知可得:余弦
A(0,0,0), B(1,0,0),C(1,1,0),
D(0,2,0), P(0,0,2), E(0,1,1),
(2)
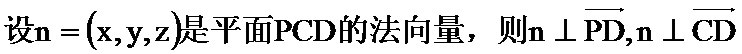
由
得
令y=1,则n=(1,1,1),
所以,所求二面角的余弦值为
解析
解析已在路上飞奔,马上就到!
知识点
21.函数


(Ⅰ)求
(Ⅱ)解关于

正确答案
解:
(Ⅰ)
由函数在

∴

∴
∴
(Ⅱ)
∵对应方程的根为
∵
∴解集为
解析
解析已在路上飞奔,马上就到!
知识点
19.在一个木制的棱长为3 的正方体表面涂上颜色,将它的棱三等分,然后从每个等分点把正方体锯开,得到27个棱长为1的小正方体,将这些小正方体充分混合后,装入一个口袋中.
(Ⅰ)从这个口袋中任意取出一个小正方体,求这个小正方体的表面恰好没有颜色的概率;
(Ⅱ)从这个口袋中同时任意取出2个小正方体,求其中一个小正方体恰好有1个面涂有颜色,另一个小正方体至少有2个面涂有颜色的概率.
正确答案
解:27个小正方体中,表面没有涂色的有1个,有一面涂色的有6个,有两面涂色的有12个,有三面涂色的有8个
(Ⅰ)
(Ⅱ)
解析
解析已在路上飞奔,马上就到!
知识点
22.已知焦点为





(Ⅰ)求
(Ⅱ)若



正确答案
解:
(1)

联立直线方程,化简为
设A(





当K不存在时,

综上,
(2)
由韦达定理知 

当
当



解析
解析已在路上飞奔,马上就到!