- 真题试卷
- 模拟试卷
- 预测试卷
6．执行下面的框图，输出的结果s的值为（ ）
A－3
B2
C
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
8．函数y=2sin（
A0
B2
C -1
D-l
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
11．给出下列命题：
①在区间（0，+∞）上，函数y=x－1，
②若logm3＜logn3＜0，则0＜n＜m＜1；
③若函数f（x）是奇函数，则f（x－1）的图象关于点A（1，0）对称；
④若函数f（x）=3x－2x－3，则方程f（x）=0有2个实数根，
其中正确命题的个数为（ ）
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
1．复数
A
B
C
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
3．已知集合A={x||2x+1|＞3}，B={x|x2+x－6≤0}，则A∩B=（ ）
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
4．已知函数f（x）=
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
5．已知sin（
A
B
C
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
7．已知向量
A－3
B
C
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
2．命题P：将函数y=sin2x的图象向右平移
命题Q：函数
则复合命题“P或Q”“P且Q”“非P”为真命题的个数是（ ）
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
10．已知向量
A以（
B以（
C以（
D以（
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
12．已知函数f（x）=x3+ax2+bx+c有两个极值点x1，x2，若f（x1）=x1＜x2，则关于x的方程3（f（x））2+2af（x）+b=0的不同实根个数为（ ）
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
9．已知函数f（x）=
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
14．已知矩形ABCD中，AB=2，AD=1，E、F分别是BC、CD的中点，则（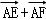
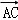
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
16．给出定义：若
①y=f（x）的定义域是R，值域是
②点（k，0）是y=f（x）的图象的对称中心，其中k∈Z；
③函数y=f（x）的最小正周期为1；
④函数y=f（x）在
则上述命题中真命题的序号是__________．
正确答案
①③
解析
解析已在路上飞奔，马上就到！
知识点
13．已知△ABC中，AB=
正确答案
2
解析
解析已在路上飞奔，马上就到！
知识点
15．已知向量
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
18．已知函数f（x）=sinx+acosx的一个零点是
（Ⅰ）求实数a的值；
（Ⅱ）设g（x）=[f（x）]2－2sin2x，求g（x）的单调递增区间．
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
19．已知函数f（x）=x3+（a+1）x2+a（2－a）x+b（a，b∈R）．
（1）若函数f（x）的图象过原点，且在原点处的切线斜率是－3，求a，b的值；
（2）若函数f（x）在区间（－1，1）上不单调，求a的取值范围．
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
20．已知A、B、C的坐标分别为A（4，0）、B（0，4）、C（3cosα，3sinα）
（Ⅰ）若a∈（－π，0），且|
（Ⅱ）若
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
21．已知a∈R，函数f（x）=x2（x－a）．
（Ⅰ）当a=3时，求f（x）的零点；
（Ⅱ）求函数y=f （x）在区间[1，2]上的最小值．
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
22．已知函数
（Ⅰ）当a=2时，求曲线y=f（x）在点（1，f（1））处的切线方程；
（Ⅱ）求函数f（x）的单调区间；
（Ⅲ）若对任意的x∈[1，+∞），都有f（x）≥0成立，求a的取值范围．
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
17．已知p：x2－8x－20≤0，q：x2－2x+1－m2≤0（m＞0）．若p是q的必要不充分条件，求实数m的取值范围．
正确答案
解析
解析已在路上飞奔，马上就到！