- 真题试卷
- 模拟试卷
- 预测试卷
1.命题“
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.已知某个几何体的三视图如下,根据图中标出的尺寸(单位:cm),可得这个几何体的体积是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.已知函数

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2.关于命题p:

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.已知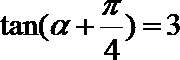
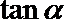
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.已知

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.变量x,y满足

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.函数
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.在平面直角坐标系中,横坐标、纵坐标均为整数的点称为整点,如果函数f(x)的图象恰好通过n(
① 
②
③ 
④
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9. 以双曲线
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.已知长方体从同一顶点出发的三条棱的长分别为1、2、3,则这个长方体的外接球的表面积为_____________.
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14.点P(2,-1)为圆
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12.设


正确答案
5
解析
解析已在路上飞奔,马上就到!
知识点
13.已知点A(m,n)在直线

正确答案
4
解析
解析已在路上飞奔,马上就到!
知识点
15.对于正项数列




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.已知关于x的一元二次函数
(1)设集合P={1,2,3},和Q={-1,1,2,3,4,},分别从集合P和Q中随机取一个数作为a和b,求函数y=f(x)在区间[1,+
(2)设点(a,b)是区域
正确答案
(1)


要使

当且仅当
若
若a=2则b= -1,1
若a=3则b= -1,1
记B={函数y=f(x)在区间[1
则事件B包含基本事件的个数是1+2+2=5,
(2)依条件可知试验的全部结果所构成的区域为

其面积
事件A构成的区域:
A=
由
得交点坐标为(


解析
解析已在路上飞奔,马上就到!
知识点
19.如图,四边形ABCD为矩形,DA
(1)求证:
(2)求四棱锥E-ABCD的体积;
(3)设点M在线段AB上,且AM=MB,试在线段CE上确定一点N,使得MN//平面DAE。
正确答案
(1)因为
所以
因为
因为

则
因为
则DE
(2)作
因为
(3)因为BE=BC,
所以F是BC的中点
设P是BE的中点,连接MP,FP
所以MP//AE,FP//DA
因为
解析
解析已在路上飞奔,马上就到!
知识点
18.设同时满足条件:①






(1)求{
(2)设


正确答案
(1)因为
当



(2)由(1)知,

若
则有
而
故
解得
再将

所以
由于①
(或做差更简单:
因为
所以
②

所以符合①②,故
解析
解析已在路上飞奔,马上就到!
知识点
20.已知函数
(Ⅰ)如果函数

(Ⅱ)是否存在正实数a,使得函数

正确答案
(Ⅰ)当a=0时,

当a


由于

所以

综上,a的取值范围是
(Ⅱ)
因F(x)在区间(
所以
即方程

设
令


当

当

为满足题意,只需

故
解得
解析
解析已在路上飞奔,马上就到!
知识点
21.已知椭圆C:


(I)求椭圆C的方程;
(II)已知动直线
①若线段AB中点的横坐标为
②已知点M(

正确答案
(I)因为


解得
则椭圆方程为
(II)①将

因为AB中点的横坐标为-
所以
②由①知
所以
=
=
=
=
解析
解析已在路上飞奔,马上就到!
知识点
17.已知函数



(1)若
(2)若


正确答案
(1)
=
f(C)=
因为

由余弦定理知:
因
b=3a
解得:a=1,b=3
(2)由条件知
所以
所以
因为
所以


于是
解析
解析已在路上飞奔,马上就到!





















































































