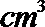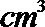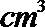文科数学攀枝花市2013年高三试卷

精品

单选题
填空题
简答题

立即下载

文科数学热门试卷

X 查看更多试卷

试卷目录

1、单选题

2、填空题

3、简答题

真题试卷
模拟试卷
预测试卷

单选题本大题共10小题，每小题5分，共50分。在每小题给出的4个选项中，有且只有一项是符合题目要求。

题型：单选题

分值: 5分

2．设集合,，则等于（）

A[-1,1]

B(-1,0)

C[1,3)

D(0,1)

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

直线与平面平行的判定与性质

题型：单选题

分值: 5分

3．“”是“方程表示焦点在轴上的椭圆”的（）

A充分不必要条件

B必要不充分条件

C充要条件

D既不充分也不必要条件

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

复合函数的单调性

题型：单选题

分值: 5分

4．已知是两条不同的直线，是两个不同的平面，则下列命题中不正确的是（）

A若则

B若则

C若，则

D若，则

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

直线、平面垂直的综合应用

题型：单选题

分值: 5分

6．已知抛物线的焦点与双曲线的一个焦点重合，则该双曲线的离心率为（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

求函数y＝Asin(ωx＋φ)的解析式

题型：单选题

分值: 5分

9．过抛物线的焦点的直线交抛物线于两点，为坐标原点，若，则的面积为（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

空间图形的公理

题型：单选题

分值: 5分

1．在复平面内，复数（是虚数单位）所对应的点位于（）

A第一象限

B第二象限

C第三象限

D第四象限

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

相等向量与相反向量

题型：单选题

分值: 5分

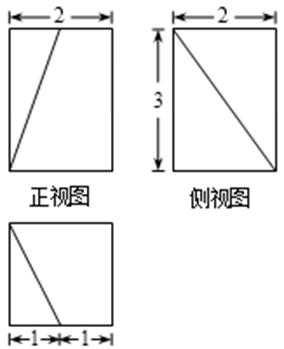
7．已知某几何体的三视图(单位:cm)如图所示，则该几何体的体积为（）

B10

C11

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

平行公理

题型：单选题

分值: 5分

8．关于函数，下列结论中不正确的是（）

A在区间上单调递增

B的一个对称中心为

C的最小正周期为

D当时,的值域为

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

三角函数中的恒等变换应用

题型：单选题

分值: 5分

5．设是等差数列的前项和，若，则＝（）

B－1

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

等差数列的基本运算等差数列的性质及应用等差数列的前n项和及其最值

题型：单选题

分值: 5分

10．已知函数是定义在R上的奇函数，若对于任意给定的不等实数，不等式恒成立，则不等式的解集为（）

A（1，＋）

B（一，0）

C（0，＋）

D（一，1）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

函数单调性的判断与证明奇偶性与单调性的综合其它不等式的解法

填空题本大题共5小题，每小题5分，共25分。把答案填写在题中横线上。

题型：填空题

分值: 5分

11．某程序框图如图所示，则该程序运行后输出的值为_________．

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

程序框图

题型：填空题

分值: 5分

12．已知实数满足，则的最小值是________．

正确答案

-5

解析

解析已在路上飞奔，马上就到！

知识点

求线性目标函数的最值

题型：填空题

分值: 5分

13．已知向量，满足，则向量与的夹角为___________.

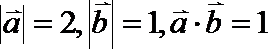
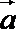
正确答案

解析

解析已在路上飞奔，马上就到！

知识点

向量的模平面向量数量积的运算数量积表示两个向量的夹角

题型：填空题

分值: 5分

15．已知表示大于的最小整数，例如．下列命题:

①函数的值域是；

②若是等差数列，则也是等差数列；

③若是等比数列，则也是等比数列；

④若，则方程有个根．

其中正确的的序号是 ____________ ．（把你认为正确的序号都填上）

正确答案

①④

解析

解析已在路上飞奔，马上就到！

知识点

命题的真假判断与应用函数的值域及其求法函数零点的判断和求解等差数列的判断与证明等比数列的判断与证明

题型：填空题

分值: 5分

14．已知且满足，则的最小值为_____________．

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

对数的运算性质利用基本不等式求最值

简答题（综合题）本大题共75分。简答应写出文字说明、证明过程或演算步骤。

题型：简答题

分值: 12分

16．在△ABC中，角A，B，C的对边分别为a，b，c．设向量，．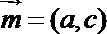

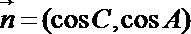
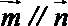
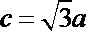
（1）若，，求角A；

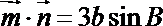
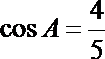
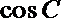
（2）若，，求的值．

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

平行向量与共线向量平面向量的坐标运算平面向量数量积的运算向量在几何中的应用

题型：简答题

分值: 12分

18．如图，在直三棱柱中，AB⊥BC，E，F分别是，的中点．

（1）求证：EF∥平面ABC；

（2）求证：平面⊥平面；

（3）若，求三棱锥的体积．

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

棱柱、棱锥、棱台的体积直线与平面平行的判定与性质平面与平面垂直的判定与性质

题型：简答题

分值: 12分

19．在数列中，。

（I）证明是等比数列，并求的通项公式；

（II）求的前n项和。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

由递推关系式求数列的通项公式等比数列的判断与证明错位相减法求和

题型：简答题

分值: 13分

20．已知椭圆C：的一个焦点是（1，0），两个焦点与短轴的一个端点构成等边三角形．

（1）求椭圆C的方程；

（2）过点Q（4，0）且不与坐标轴垂直的直线l交椭圆C于A、B两点，设点A关于x轴的对称点为。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

椭圆的定义及标准方程椭圆的几何性质直线与圆锥曲线的综合问题圆锥曲线中的范围、最值问题圆锥曲线的定点、定值问题

题型：简答题

分值: 12分

17．在某高校自主招生考试中，所有选报II类志向的考生全部参加了“数学与逻辑”和“阅读与表达”两个科目的考试，成绩分为A,B,C,D,E五个等级．某考场考生的两科考试成绩数据统

计如下图所示，其中“数学与逻辑”科目的成绩为B的考生有10人．

（1）求该考场考生中“阅读与表达”科目中成绩为A的人数；

（2）若等级A，B，C，D，E分别对应5分，4分，3分，2分，1分，求该考场考生“数学与逻辑”科目的平均分；

（3）已知参加本考场测试的考生中，恰有两人的两科成绩均为A．在至少一科成绩为A的考生中，随机抽取两人进行访谈，求这两人的两科成绩均为A的概率．

正确答案

解: (1)因为“数学与逻辑”科目中成绩等级为B的考生有10人，

所以该考场有人

所以该考场考生中“阅读与表达”科目中成绩等级为A的人数为，

（2）该考场考生“数学与逻辑”科目的平均分为

（3）因为两科考试中，共有6人得分等级为A，又恰有两人的两科成绩等级均为A，

所以还有2人只有一个科目得分为A，

设这四人为甲，乙，丙，丁，其中甲，乙是两科成绩都是A的同学，则在至少一科成绩等级为A的考生中，随机抽取两人进行访谈，基本事件空间为

{甲，乙}，{甲，丙}，{甲，丁}，{乙，丙}，{乙，丁}，{丙，丁},有6个基本事件

设“随机抽取两人进行访谈，这两人的两科成绩等级均为A”为事件B，所以事件B中包含的基本事件有1个，则.

解析

解析已在路上飞奔，马上就到！

知识点

古典概型的概率众数、中位数、平均数

题型：简答题

分值: 14分

21．已知函数，．

（1）当时，求函数的极大值；

（2）求函数的单调区间；

（3）当时，设函数，若实数满足：且，，求证：．

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

利用导数研究函数的单调性利用导数求函数的极值利用导数求函数的最值利用导数证明不等式

文科数学 热门试卷

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

文科数学热门试卷