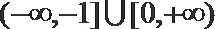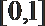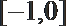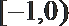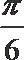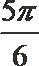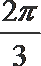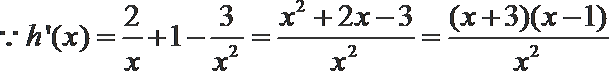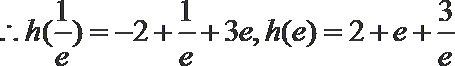- 真题试卷
- 模拟试卷
- 预测试卷
6. 从某项综合能力测试中抽取100人的成绩,统计如表,则这100人成绩的标准差为( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2. 已知i是虚数单位,则
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7. 在区间

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.函数
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.已知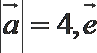
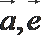
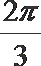
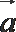
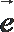
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.设

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.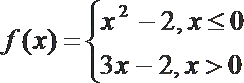
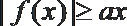
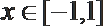
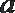
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
1.设集合


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
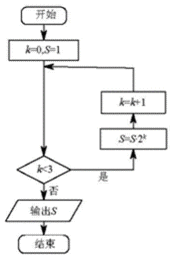
5.执行如图所示的程序框图,输出的S值为( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.某三棱锥的三视图如上图所示,该三棱锥的体积是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.定义式子运算为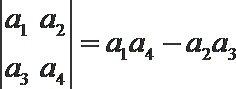
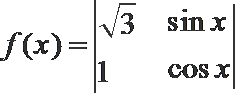
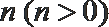
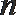
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12.已知


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15.如图,正六边形ABCDEF的两个顶点A、D为双曲线的焦点,其余四个顶点都在双曲线上,则该双曲线的离心率为_____。
正确答案

解析
解析已在路上飞奔,马上就到!
知识点
13.设



正确答案
1
解析
解析已在路上飞奔,马上就到!
知识点
14.在正三棱锥S-ABC中,侧面SAB、侧面SAC、侧面SBC两两垂直,且侧棱

正确答案
36π
解析
解析已在路上飞奔,马上就到!
知识点
16. 函数



正确答案
64
解析
解析已在路上飞奔,马上就到!
知识点
20.已知动圆过定点A(0,2), 且在x轴上截得的弦长为4。
(1) 求动圆圆心的轨迹C的方程;
(2)点P为轨迹C上任意一点,直线l为轨迹C上在点P处的切线,直线l交直线:y=-1于点R,过点P作PQ⊥l交轨迹C于点Q,求△PQR的面积的最小值。
正确答案
(1)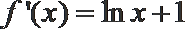
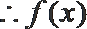
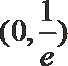
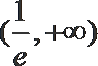
①当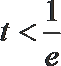
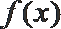
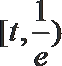
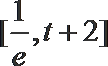
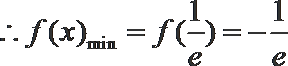
②当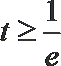
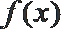
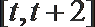
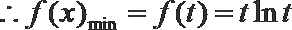
(2)由题意可知,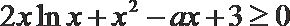
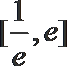
即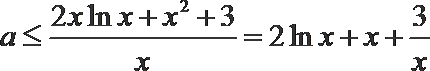
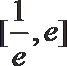
令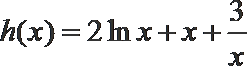
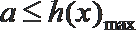
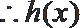
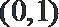
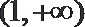
则在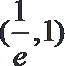
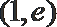
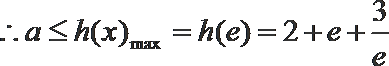
解析
解析已在路上飞奔,马上就到!
知识点
19.在长方体

(1)求证:

(2)在棱

正确答案
(1)在长方体



在矩形


所以

(2)当点



理由如下:在


因为



所以


又





所以四边形


又





解析
解析已在路上飞奔,马上就到!
知识点
17.在



(1)求角
(2)若

正确答案
(1)由

所以
(2) 由余弦定理a2=b2+c2-2bccos A,得b2+c2-bc=36.又b+c=8,所以bc=
由三角形面积公式S=

解析
解析已在路上飞奔,马上就到!
知识点
18、某种产品的广告费支出x与销售额y(单位:万元)之间有如下对应数据:
(1)求回归直线方程;
(2)试预测广告费支出为10万元时,销售额多大?
(3)在已有的五组数据中任意抽取两组,求至少有一组数据其预测值与实际值之差的绝对值不超过5的概率。(参考数据: 
正确答案
(1)



因此,所求回归直线方程为:
(2)根据上面求得的回归直线方程,当广告费支出为10万元时,
(3)
基本事件:(30,40),(30,60),(30,50),(30,70),(40,60),(40,50),(40,70),(60,50),(60,70),(50,70)共10个,
两组数据其预测值与实际值之差的绝对值都超过5的有(60,50),
所以至少有一组数据其预测值与实际值之差的绝对值不超过5的概率为
解析
解析已在路上飞奔,马上就到!
知识点
21.已知函数

(1)求函数

(2)若存在



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
22.选考题:请考生在第1、2、3题中任选一题做答,如果多做,则按所做的第一题记分。
1.如图,







(1)
(2)
2.在直角坐标系中,以原点为极点,








(1)写出曲线

(2)若

3.已知函数


(1)求
(2)解关于

正确答案
1.
证明:(1)因为

又已知


而


故


(2)因为


而
故
2.
(1)C:
(2)将直线的参数表达式代入抛物线得

3.
(1)∵
∴
(2)当

当

当

综上:此不等式的解集为
解析
解析已在路上飞奔,马上就到!