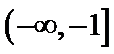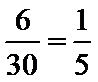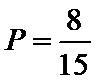- 真题试卷
- 模拟试卷
- 预测试卷
1.复数z=
正确答案
解析
z=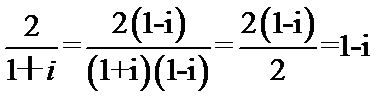
考查方向
解题思路
分母实数化,同时乘以分母的共轭复数化简即可。
易错点
分母不知道怎么实数化。
知识点
2.设集合A={x|1<x<2},B={x|x<a},若A∩B=A,则a的取值范围是
正确答案
解析
由A∩B=A,可知A是B的子集,所以a≤2,选D。
考查方向
解题思路
由题意可知A是B的子集,然后求出a的取值范围。
易错点
不会由已知条件转化为2个集合之间的关系。
知识点
4.实数a=3是直线ax+2y+3a=0和直线3x+(a-1)y-a+7=0平行的
正确答案
解析
由a=3显然可以得到直线ax+2y+3a=0和直线3x+(a-1)y-a+7=0平行,但是反过来直线ax+2y+3a=0和直线3x+(a-1)y-a+7=0平行得到a=3或者a=-2,所以选A。
考查方向
解题思路
从左往右和从右往左依次来判断。
易错点
平行的时候用斜率做漏掉斜率不存在。
知识点
6.已知实数x、y满足约束条件

正确答案
解析
如下图所示:



考查方向
解题思路
先画出可行域,再用数形结合法找到斜率的取值范围。
易错点
不会将目标函数转化为斜率来求解。
知识点
9.已知某几何体的三视图如图所示,根据图中标出的尺寸,可得这个几何体的表面积是
正确答案
解析
直观图如图所示
所以表面积为底面的面积加上4个侧面积,可得表面积为 5+2

考查方向
解题思路
先由三视图还原出直观图再求出其表面积。
易错点
不知道直观图是一个什么几何体。
知识点
3.在等差数列{



正确答案
解析
由



考查方向
解题思路
根据已知条件来求,将式子全部化为只含公差和首项的方程,最后即可得到要求的值。
易错点
不会根据已知条件来求。
知识点
5.执行如图所示的程序框图,若输入n的值为6,则输 出s 的值是
正确答案
解析
s=1
考查方向
解题思路
按照顺序依次执行,直到满足条件跳出循环得到结果。
易错点
跳出循环错误。
知识点
7.若直线2ax-by+2=0(a>0,b>0)被圆


正确答案
解析
由已知可知弦长为4即为直径,所以直线过原点,即满足a+b=1,所以

考查方向
解题思路
根据已知条件找到a和b的一个关系式,再与要求的式子联系起来使用基本不等式即可解出。
易错点
要求的式子的最值不会转化。
知识点
8.已知双曲线

正确答案
解析
抛物线的焦点为(3,0),所以c=3,而a=2,则


考查方向
解题思路
由抛物线的方程求出焦点然后进一步求出双曲线中的未知数b,然后利用点到直线的距离公式即可解出。
易错点
焦点求错。
知识点
10.已知点P是函数y=sin(2x+θ)图像与x轴的一个
交点,A,B为P点右侧同一周期上的最大值和最小
值点,则

正确答案
解析
可以考虑特殊情况,即当θ=0时来做,故p可以选择原点,AB两点的坐标也很容易表示出来,所以利用向量的数量积的坐标运算可得


考查方向
解题思路
可以找一种特殊情况来做。
易错点
不会求其数量积。
知识点
11.如图(3)所示,侧棱与底面垂直,且底面为正方形的四棱柱ABCD-A1B1C1D1中,AA1=2,AB=1,M、N分别在AD1、BC上移动,始终保持MN∥平面DCC1D1,设BN=x,MN=y,则函数y=f(x)的图像大致是
正确答案
解析
由题意可知,函数的解析式是
考查方向
解题思路
作出辅助线,找到两者之间的关系,从而找到函数满足的图像。
易错点
y与x之间的函数关系式不会求。
知识点
12.函数f(x)=
正确答案
解析







考查方向
解题思路
转化为求函数在区间[0,1]上的最小值。
易错点
恒成立的问题不会转化。
知识点
13.将参加中国好声音的500名大众评委编号为001,002,…,500.先采用系统抽样方法抽取一个容量为20的样本,若随机抽得的号码为003,那么抽中的20个样本编号由小到大排列,第5个号码是___________.
正确答案
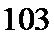
解析
看成是首项为3,公差是20的等差数列求第5项,所以第5个号码是103.
考查方向
解题思路
本题考查系统抽样,可以看成是一个等差数列即可解出。
易错点
等间隔抽样搞错其中的项数。
知识点
15.椭圆
正确答案

解析
由题意可以得4a=12,所以a=3,c=2,所以该椭圆的离心率是
考查方向
解题思路
根据焦点在x轴,所以a>
易错点
什么时候取到周长的最大值不清楚。
知识点
16.已知函数y=f(x)为R上的偶函数,y=f(x)的导数为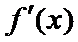
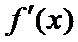
[-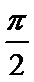
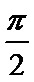
正确答案
解析
构造函数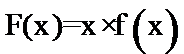
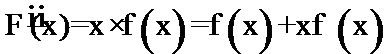
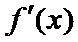
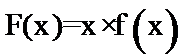
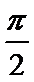

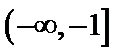
考查方向
解题思路
先构造函数,然后利用所构造的函数将已知要求的参数的取值范围转化为求函数的最值问题。
易错点
不知道构造函数来解答。
知识点
14.已知向量a=(x-1,2),b=(4,y),若a⊥b,则点P(x,y)到原点的距离的最小值为___________.
正确答案

解析
由已知得

考查方向
解题思路
本题考查向量数量积的坐标运算,根据已知得到一个二元一次方程,最后转化为原点到这条直线的距离来解答。
易错点
点p到原点的距离不知道怎么来解答。
知识点
17. 已知函数f(x)=2

(Ⅰ)求函数f(x)的对称轴所在的直线方程;
(Ⅱ)在△ABC中,a,b,c分别是角A,B,C的对边,且f(C)=3,c=1,ab=2
且a<b,求a,b的值.
正确答案
(1)

解析
试题分析:本题属于简单的三角恒等变换及正余弦定理解三角型的问题,(1)先用辅助角公式化简再进一步求解,(2)利用余弦定理最后再构造方程组来解答。
17解:(Ⅰ)
对称轴所在的直线方程为:
(Ⅱ) 

∴

∴
由


∴



考查方向
解题思路
本题考查简单的三角恒等变换及正余弦定理解三角型,解题步骤如下:(1)先用辅助角公式化简再进一步求解,(2)利用余弦定理最后再构造方程组来解答。
易错点
不会使用辅助角公式合二为一。
知识点
20. 已知椭圆


(Ⅰ)求椭圆的方程;
(Ⅱ)设A、B分别为椭圆的左、右顶点,过点F且斜率为k的直线与椭圆交于C,D两点.若



正确答案
(1)+=1;(2)
解析
试题分析:本题属于直线和圆锥曲线的位置关系,题目的难度是逐渐由易到难,
(1)根据题目已知条件构造方程组即可求出;
(2)设出直线的方程,与第一问所求的椭圆方程联立起来消元后得到一个一元二次方程,再应用设而不求的方法得到一个方程就可以解出来。解: (1)设F(-c,0),由=,知a=c.过点F且与x轴垂直的直线为x=-c,
代入椭圆方程+=1,解得y=±b,
于是b= ,解得b=,
又a2-c2=b2,从而可得a=,c=1,
所以椭圆的方程为+=1. (2)设点C(x1,y1),D(x2,y2),由F(-1,0)得直线CD的方程为y=k(x+1),
由方程组
因为直线过椭圆内的点,无论k为何值,直线和椭圆总相交.
由根与系数的关系可得: 则x1+x2=-,x1x2=,因为A(-,0),B(,0),所以
·+·=(x1+,y1)·(-x2,-y2)+(x2+,y2)·(-x1,-y1)
=6-2x1x2-2y1y2=6-2x1x2-2k2(x1+1)(x2+1)
=6-(2+2k2)x1x2-2k2(x1+x2)-2k2
=6+, 由已知得6+=7,解得
考查方向
解题思路
本题考查直线和圆锥曲线的位置关系,解题步骤如下:
(1)根据题目已知条件构造方程组即可求出;
(2)设出直线的方程,与第一问所求的椭圆方程联立起来消元后得到一个一元二次方程,再应用设而不求的方法得到一个方程就可以解出来。
易错点
不会使用设而不求的方法去解答。
知识点
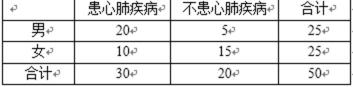
18. 近年空气质量逐步恶化,雾霾天气现象出现增多,大气污染危害加重.大气污染可引起心悸、呼吸困难等心肺疾病.为了解某市心肺疾病是否与性别有关,在某医院随机对入院的50人进行了问卷调查得到了如下的列联表:
(Ⅰ)用分层抽样的方法在患心肺疾病的人群中抽6人,再从6人中选2人,求恰有一名女性的概率?
(Ⅱ)为了研究心肺疾病是否与性别有关,请计算出统计量K2,你有多大的把握认为心肺疾病与性别有关?
下面的临界值表供参考:
正确答案
(1)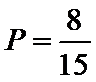
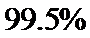
解析
试题分析:本题属于考查了分层抽样和古典概型以及独立性检验,(1)先利用分层抽样的方法计算出男女各抽多少人,然后利用古典概型公式计算;(2)利用独立性检验的方法来解(Ⅰ)解:在患心肺疾病人群中抽6人,则抽取比例为
∴ 女性应该抽取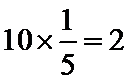
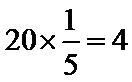
女性2人记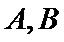
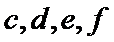
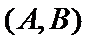
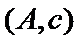
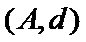
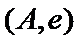

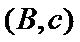
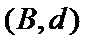
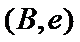
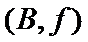
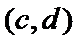
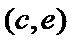
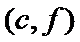
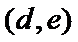
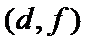
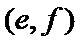
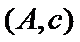
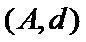
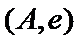
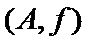
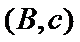
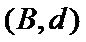
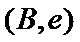
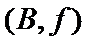
故上述抽取的6人中选2人,恰有一名女性的概率概率为
(Ⅱ):∵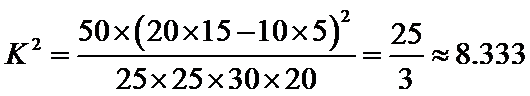
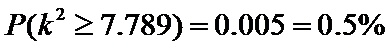
那么,我们有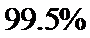
考查方向
解题思路
本题考查古典概型和独立性检验,解题步骤如下:(1)先利用分层抽样的方法计算出男女各抽多少人,然后利用古典概型公式计算;(2)利用独立性检验的方法来解。
易错点
分类容易遗漏。
知识点
19. 如图,在矩形ABCD中,AB=2,AD=1,M为DC的中点.将△ADM沿AM折起,使得平面ADM⊥平面ABCM.
(Ⅰ)若E为BD的中点,求证:
正确答案
(1)见解析;(2)
解析
试题分析:本题属于立体几何的证明与体积的计算问题,
(1)由已知条件然后结合线面平行的判定定理来证明;
(2)将底面换了之后再来计算其体积。
(1)证明:取



又






(2)在平面图形




考查方向
解题思路
本题考查立体几何的证明与体积的计算问题,解题步骤如下:
(1)由已知条件然后结合线面平行的判定定理来证明;
(2)将底面换了之后再来计算其体积。
易错点
不会换底去计算体积。
知识点
21.设函数f(x)=lnx+
(Ⅰ)当a=
(Ⅱ)当x>1时,若f(x)<
正确答案
(1)



(2)
解析
试题分析:本题属于导数求含参数的函数的单调区间及参数的取值范围的问题,题目的难度是逐渐由易到难,
(1)利用导数与函数的单调性的关系直接求解;
(2)构造函数,再利用导数并分参数a在几类情况下分类来解解:(1)当










(2)

令


当







当

当








当









而



综上:
考查方向
解题思路
本题考查导数求含参数的函数的单调区间及参数的取值范围的问题,解题步骤如下:
(1)利用导数与函数的单调性的关系直接求解;
(2)构造函数,再利用导数并分参数a在几类情况下分类来解。
易错点
第2问不知道怎样转换已知条件。
知识点
22.如图(8),圆O1与圆O2相交于A、B两点,AB是圆O2的直径,过A点作圆O1的切线交圆O2于点E,并与BO1的延长线交于点P,PB分别与圆O1、圆O2交于C,D两点.
(Ⅰ)求证:PA·PD=PE·PC;
(Ⅱ)求证:AD=AE.
正确答案
(1)见解析;(2)见解析
解析
试题分析:本题属于几何证明选讲中的证明问题,
(1)由切割线定理直接证明;(2)直接按照步骤来求。



又

由①,②得
(2)连接AC,DE, 
由(1)知,
AB是⊙O2的直径,
考查方向
解题思路
本题考查几何证明选讲中的证明问题,解题步骤如下:
(1)由切割线定理直接证明;
(2)直接按照步骤来求。
易错点
图形看不懂,比较复杂。