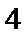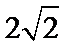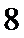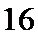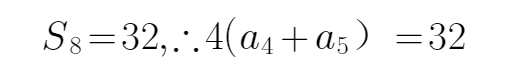- 真题试卷
- 模拟试卷
- 预测试卷
2.已知复数


正确答案
解析
由题意可知,

考查方向
复数的概念和性质,共轭复数的计算
解题思路
先求出z的表达式,然后求其共轭复数
易错点
不理解复数的概念,计算错误
知识点
3.
正确答案
解析
由已知可知,

考查方向
充要条件的判定
解题思路
根据所给条件,结合选项判断
易错点
充分条件、必要条件判断错误
知识点
4.如图所示的算法框图中,


正确答案
解析
由题意知,得
,而
则输出的i值为8,所以选D
考查方向
程序框图
解题思路
按照算法框图,顺序结构和条件判断语句求出答案
易错点
判断语句判断错误
知识点
5.双曲线




正确答案
解析
由已知可知,
故选A
考查方向
双曲线的性质,双曲线的渐近线方程
解题思路
根据渐近线方程求出参数的关系,然后求出离心率
易错点
找不到双曲线参数之间的关系
知识点
8.已知函数









正确答案
解析
由已知,f(x)在


考查方向
偶函数的性质
函数的增减性
解题思路
先求出a.b.c的值,然后判断大小
易错点
根据指数的运算性质和对数的运算性质计算
知识点
1.已知集合


正确答案
解析
由题意可知,
所以
考查方向
集合的运算,求集合的交集
解题思路
分别求出A和B集合所表示出来的元素。然后求交集
易错点
求交集错误
知识点
6.已知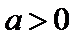
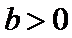
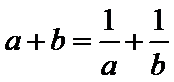
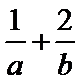
正确答案
解析
由已知可知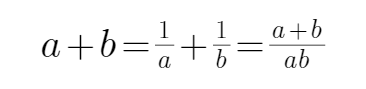
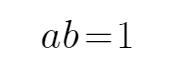
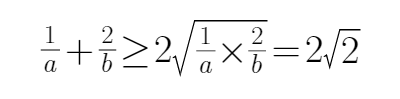
考查方向
平均值不等式的性质
解题思路
利用均值不等式求最小值
易错点
找不到“一正、二定、三相等”条件
知识点
7.一个几何体的三视图如图所示,则该几何体的表面积等于( )
正确答案
解析
由三视图可知,该几何体为底面直径为3,高为4的圆柱与它的外接球组成的几何体,球的直径为5,所以表面积为25,选D
考查方向
根据几何体的三视图还原成立体图形
求几何体的表面积
解题思路
先还原成立体图形,然后求其表面积
易错点
空间感不强,计算错误
知识点
10.已知函数




正确答案
解析
由图象可知,A=2,


考查方向
三角函数的图象的性质和特征
解题思路
根据所给图象求出未知参数,进而得到函数的递增区间
易错点
计算错误,对三角函数的图象性质掌握不好
知识点
9.中国古代文数著作《算法统宗》中有这样一个问题:“三百七十八里关,初步健步不为难,次日脚痛减一半,六朝才得到其关,要见次日行里数,请公仔细算相还.”其大意为:“有一个人走

正确答案
解析
记每天走的路程里数为an,易知an是公比
所以
考查方向
等比数列求和
解题思路
利用等比数列求和,然后求出
易错点
不能建立出正确的数学模型
知识点
12.已知函数


正确答案
解析
由题意可知,结合函数图象可以知道,
所以可以看出,答案为D
考查方向
分段函数的图象
解题思路
结合图象作出图象,即可
易错点
作图象错误,对函数的性质掌握不牢固
知识点
11.





正确答案
解析

因为AD垂直BC,a垂直b,所以
考查方向
平面向量的运算
解题思路
根据已知条件,结合选项依次判断
易错点
对平面向量的知识点掌握不好,计算错误
知识点
16.已知抛物线









正确答案
3
解析
由题意可知,

考查方向
抛物线的几何性质,抛物线与直线的结合题
解题思路
根据抛物线的定义,够造出FQ的表达式,然后求出最小值
易错点
计算错误,圆锥曲线性质掌握不好
知识点
14.若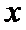

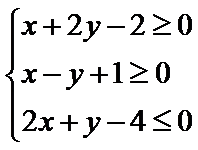
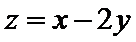
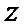
正确答案
[-3,2]
解析
有题意可知,作图可以知道,在点(2,0)处取最大值2,在点(1,2)处取最小值-3
考查方向
线性规划的简单应用
解题思路
先作出可行域,然后找到最值点,求出最值
易错点
作图错误,找点错误
知识点
13.设等差数列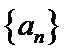
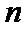
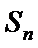
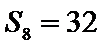

正确答案
16
解析
由题意可知,
考查方向
等差数列的前n项和
解题思路
根据等差数列的性质,求出答案
易错点
不理解等差数列的性质和运算
知识点
15.某学校高二年级共有女生


正确答案
56.5
解析
由题意可知,平均数为:
考查方向
统计数的平均数
解题思路
根据统计频率分布直方图,得到各个数据,然后求其平均数
易错点
找数据马虎,计算错误
知识点
已知圆



23.求椭圆
24.椭圆






正确答案
详见解析
解析
(Ⅰ) 圆
圆心坐标为
过椭圆










考查方向
直线与圆的方程,求椭圆的标准方程
解题思路
先求出直线L的方程,然后求出a b c进而求出椭圆的标准方程
易错点
计算能力弱,相关公式定理混淆
正确答案
详见解析
解析
(Ⅱ)由(Ⅰ)知


由




考查方向
直线与圆锥曲线的结合题,直线的斜率
椭圆的几何性质
解题思路
设出相关参数,根据所给条件,建立方程,最后求出答案
易错点
计算能力弱,找不到恰当的等量关系
已知

17.求
18.在





正确答案
详见解析
解析

(I) 
考查方向
三角函数的周期
解题思路
根据三角函数的性质,化简成同名同角,然后求最小正周期
易错点
对三角函数的性质掌握不好,对角的范围讨论错误
正确答案
详见解析
解析
(II) 


又


在


考查方向
余弦定理,
解题思路
先求出f(A)的最大值,求出A的值,然后利用余弦定理,求出三角形ABC的面积。
随着“全面二孩”政策推行,我市将迎来生育高峰.今年新春伊始,宜城各医院产科就已经是一片忙碌,至今热度不减.卫生部门进行调查统计,期间发现各医院的新生儿中,不少都是“二孩”;在市第一医院,共有



19.从两个医院当前出生的所有宝宝中按分层抽样方法抽取
①在市第一医院出生的一孩宝宝中抽取多少个?
②若从
20.根据以上数据,能否有
正确答案
详见解析
解析
(Ⅰ)(1)由分层抽样知在市第一医院出生的宝宝有
(2) 在抽取7个宝宝中,市一院出生的一孩宝宝2人,分别记为




用

考查方向
分层抽样,随机事件发生的概率
解题思路
根据分层抽样的性质计算,
将一切可能结果分别列出来。
易错点
计算错误,考虑问题有重漏
正确答案
详见解析
解析
(Ⅱ)


考查方向
K值检验,相关度检验
解题思路
根据数据列出2X2列联表,然后求出K值,进而判断
易错点
计算能力弱
如图,圆柱











21.求证:平面

22.若


正确答案
详见解析
解析
(Ⅰ)由已知,






考查方向
线面垂直的性质与判定,面面垂直的性质与判定
解题思路
根据题意,由线面垂直证明面面垂直
易错点
空间感弱,逻辑关系混乱
正确答案
详见解析
解析
(Ⅱ)因




则四棱锥











考查方向
求几何体的体积
解题思路
根据题意,求出几何体的体积的相关线段,然后计算求得
易错点
计算能力弱,空间感弱
已知函数

25.讨论函数
26.若函数




正确答案
详见解析
解析
(Ⅰ)函数







考查方向
利用导数求函数的单调性
函数与导数的综合题
解题思路
先求出定义域,然后求导判断函数的单调区间
易错点
求导错误,分类讨论错误
正确答案
详见解析
解析
(Ⅱ)
令

令




考查方向
导数与函数的综合题
利用导数证明不等式
解题思路
先求导,然后够造出恰当的函数,利用新构造的函数的单调性,证明不等式
易错点
不能够造出正确的函数,进而不能证明不等式
选修4-1:几何证明选讲
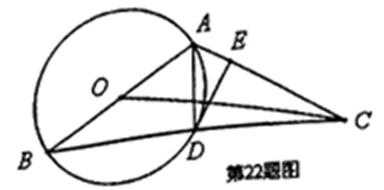
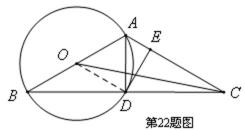
如图,以
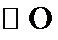
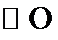
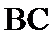
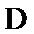
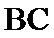
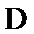
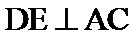
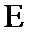
27.求证:
28.若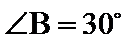
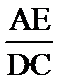
正确答案
详见解析
解析
(Ⅰ)如图,连接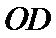
因为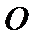
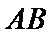
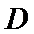
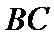
所以 
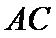
因为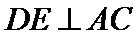
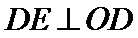
所以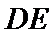
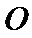
考查方向
圆的切线的性质和判断
解题思路
连接OD,根据垂直关系证明DE是圆O的切线
易错点
不能作出正确的辅助线,找不到垂直关系
正确答案
详见解析
解析
(Ⅱ)因为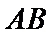
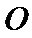
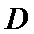
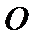

又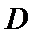
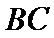
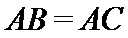
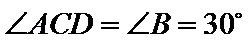
因为
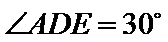
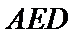
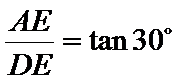
在直角三角形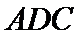
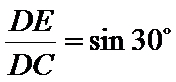
于是
考查方向
与圆有关的比例线段
相似三角形的性质和判定
解题思路
根据直角三角形中的比例线段,求出答案
易错点
找不到相似条件,不能求出正确的答案