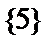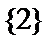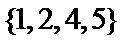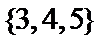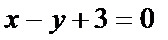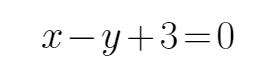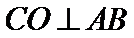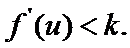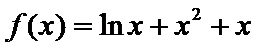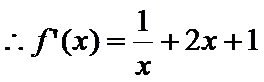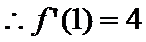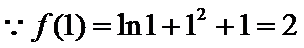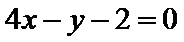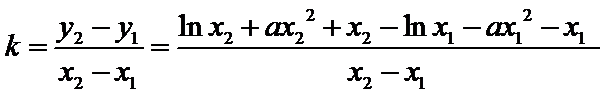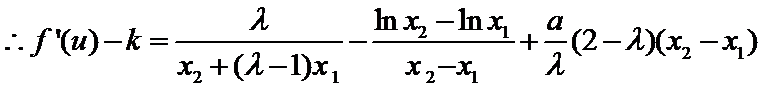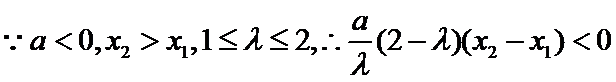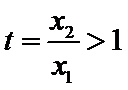- 真题试卷
- 模拟试卷
- 预测试卷
2.已知Z=
正确答案
解析

考查方向
复数的性质,复数的运算
解题思路
先化简成一般形式,然后判断其在复平面的位置
易错点
对复数的概念理解不透彻
知识点
3.已知非零向量


正确答案
解析
因为两向量平行,所以

考查方向
平面向量的数量积
向量的平行关系
解题思路
根据向量平行的性质,求解出m的值
易错点
计算错误,向量平行的数量积计算错误
知识点
12.已知抛物线






正确答案
解析
抛物线
设直线的方程为:
代入抛物线方程可得
设
由AF=3FB,得

故选C
考查方向
抛物线的性质,直线和抛物线的结合问题
解题思路
先表示出来三角形AOB的面积公式,然后求出相应的三角形的边长
易错点
计算能力弱
知识点
1.已知全集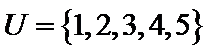
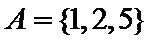
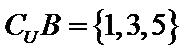
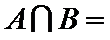
正确答案
解析
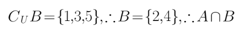
考查方向
集合的运算,集合的交集运算
解题思路
根据集合的概念求得
易错点
不理解集合的概念
知识点
11.《算数书》是我国现存最早的有系统的数学典籍,其中记载有求“囷盖”的术:置如其周,令相乘也. 又以高乘之,三十六成一. 该术相当于给出了由圆锥的底面周长L与高h,计算其体积V的近似公式



正确答案
解析
设圆锥底面圆的半径为
所以
考查方向
圆锥体积的计算
解题思路
先表示出圆锥的体积,然后反求
易错点
公式记忆不准确,化简错误
知识点
5.设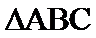
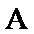
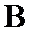
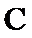
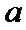
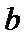
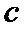
若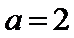
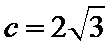
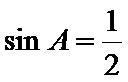

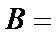
正确答案
解析
由题意可知,由正弦定理可得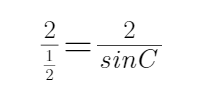
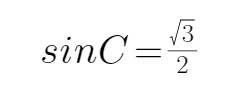
而A=30度,当C=60度时,B=90度,不符合b<c
当C=120度,B=30度,符合,所以选A
考查方向
正弦定理的性质和应用
解题思路
利用正弦定理求出角C的大小,然后求角B的大小
易错点
正弦定理公式记忆混淆
知识点
7.设函数

正确答案
解析
因为
所以
所以
考查方向
分段函数的性质,求函数的值
解题思路
按照对数函数和指数函数的计算公式依次求解
易错点
计算错误
知识点
4.执行如图所示的程序框图,输出的S值为( )
正确答案
解析
第一步,
第二步,
退出循环。
考查方向
程序框图
解题思路
按照程序框图求出输出S的值
易错点
循环条件判断错误
知识点
8.已知命题




正确答案
解析
因为P是真命题,所以非P为假命题,所以,
即


考查方向
命题的真假的判断
解题思路
根据题意依次判断命题真假
易错点
逻辑关系混乱
知识点
9. 已知函数
若将


则函数
正确答案
解析
由图可知:A=2


所以
向右平移

考查方向
三角函数的性质
三角函数的图象的变换
解题思路
根据题意求出A和T的值,然后判断其单调区间
易错点
对函数的图象的性质掌握不好
知识点
10.如图为某几何体的三视图,则该几何体的外接球的表面积为( )
正确答案
解析
由三视图知,该几何为一侧棱垂直于底面的四棱锥,底面为正方形,知其外接球半径为长方体的对角线的一半。
长方体的对角线长为:
考查方向
几何体的三视图的还原和计算
解题思路
根据三视图判断其还原后的立体图,然后求出该几何体的外接球的表面积
易错点
立体感不强,计算错误
知识点
6.设数列





正确答案
解析
根据题意可得,



考查方向
等差数列的性质
解题思路
根据题意建立等量关系,求出首项和公差,然后求出A20的值
易错点
等差数列的性质掌握不好,解方程错误
知识点
13.已知直线过圆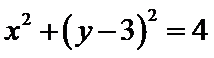
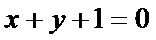
正确答案
解析
由题意可知,直线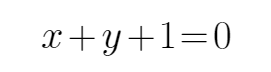
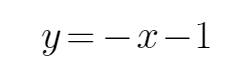
考查方向
直线与圆的关系,直线的方程
解题思路
根据直线和直线垂直,然后求直线斜率,进而求直线的方程
易错点
相关公式掌握不牢固
知识点
14.实数


正确答案
4
解析
画出不等式组表示的平面区域,如下图所示,三角形ABC为所求,目标函数化为
考查方向
线性规划求目标函数最值
解题思路
画出可行域,用目标函数判断最大值点,进而求出最大值
易错点
作图错误
知识点
15.设△ABC的内角为A,B,C,所对的边分别是



正确答案
解析
由

考查方向
余弦定理
解题思路
求出a,b,c的关系,然后利用余弦定理求角C
易错点
化简错误
知识点
16.设函数






正确答案
解析
记函数


考查方向
奇函数的性质,导数的性质和判断
解题思路
根据函数的奇偶性和单调性判断
易错点
单调性和奇偶性判断错误
知识点
已知数列






17.求数列
18.设



正确答案
详见解析
解析
(Ⅰ)设数列


由
解得
故数列

考查方向
等差数列的通项公式
解题思路
根据题意建立首项和公差的等量关系,然后求解方程求出首项和公差,然后求出通项公式
易错点
数列通项公式记忆错误
正确答案
详见解析
解析
(Ⅱ)由(1)可得
所以当

①-②得

又




考查方向
数列求和
解题思路
利用裂项相消的方法求数列的和
易错点
计算能力弱,公式定理记忆混淆
2015年8月12日天津发生危化品重大爆炸事故,造成重大人员和经济损失.某港口组织消防人员对该港口的公司的集装箱进行安全抽检,已知消防安全等级共分为四个等级(一级为优,二级为良,三级为中等,四级为差),该港口消防安全等级的统计结果如下表所示:


19.求
20.按消防安全等级利用分层抽样的方法从这
正确答案
详见解析
解析
(Ⅰ)由已知可得;0.30+2m+m+0.10=1,解得:m=0.20. ……………………2分
所以
考查方向
概率和统计的计算
解题思路
按照统计的相关数据计算
易错点
数据不敏感,计算错误
正确答案
详见解析
解析
(Ⅱ)由(Ⅰ)知,利用分层抽样的方法从中抽取10家公司,则消防安全等级为一级的有3家,二级的有4家,三级的有2家,四级的有1家. ……………………6分
记消防安全等级为二级的4家公司分别为A,B,C,D,三级的2家公司分别记为











记“抽取的2家公司的消防安全等级都是二级”为事件M,则事件M包含的结果有:(A,B)(A,C)(A,D)(B,C)(B,D)(C,D)…共6种,……………………10分
所以
考查方向
分层抽样,随机事件发生的概率
解题思路
分情况讨论所可能发生的情况,然后计算概率
易错点
先求出所有出现的可能,然后算题目要求的可能,求二者的比例
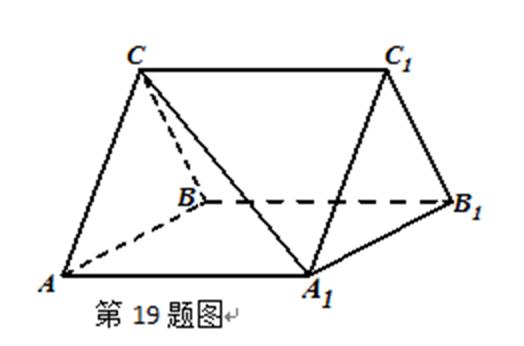
如图,三棱柱
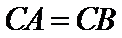
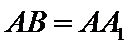
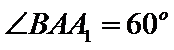
21.证明: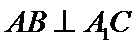
22.若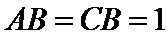
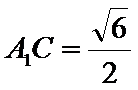
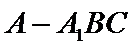
正确答案
详见解析
解析
(Ⅰ)证明:取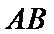
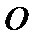
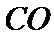

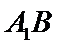

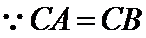
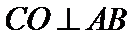
又
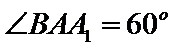
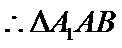
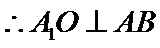
又因为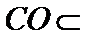
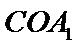
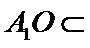
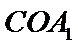
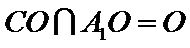
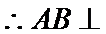
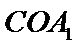
又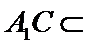
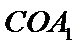
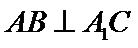
考查方向
棱柱的性质及应用,直线和直线垂直的判定
解题思路
由线面垂直证明线线垂直
易错点
空间想象力不强,逻辑性不强
正确答案
详见解析
解析
(Ⅱ)解:在等边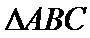
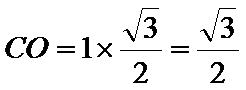
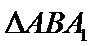
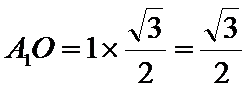
在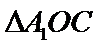
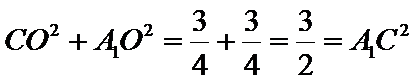
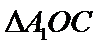
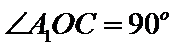
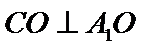
由(Ⅰ)得
又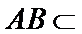
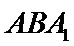
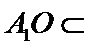
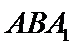
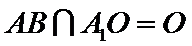
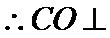
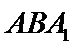
故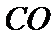
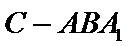
又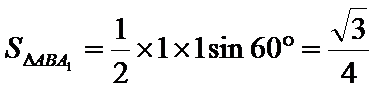
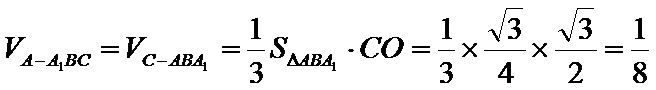
考查方向
求三棱锥的体积
解题思路
求三棱锥的底面积和高,然后计算其体积
易错点
计算能力弱,空间立体感不强
如图,圆







23.求圆
24.过点


连接

正确答案
详见解析
解析
解:(Ⅰ)设圆



∵ 



∴ 圆


考查方向
求直线和圆的方程
解题思路
先求圆C的半径,然后带入方程中,求解参数
易错点
不能正确的设出坐标,找不到等量关系
正确答案
(Ⅱ)把



即点

(1)当

(2)当



联立方程



设直线



∴
若

∵
∴ 

考查方向
直线和圆的方程,直线和圆锥曲线的综合题
解题思路
设出直线AB的方程,联立方程,消去y,然后直线AN和直线BN的斜率的和等于0,证明角相等。
已知函数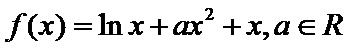
25.当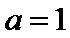
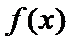
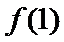
26.讨论函数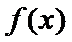
27.已知
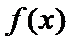
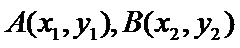
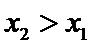

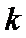
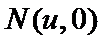
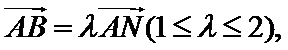
正确答案
详见解析
解析
(Ⅰ)当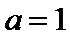
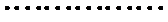
又

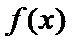


即
考查方向
导数的几何意义和切线方程
解题思路
先求导,代入a=1,然后求出切线的方程
易错点
计算能力弱,求导错误
正确答案
详见解析
解析
(Ⅱ)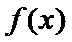
当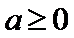
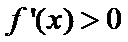
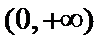
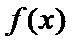
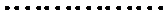
当

则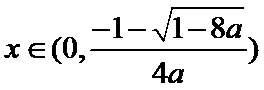
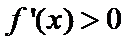
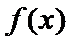
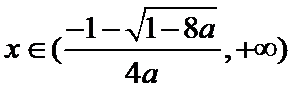
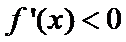
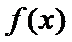
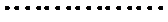
综上,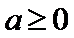


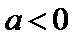
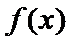
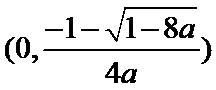


考查方向
导数和函数的综合题
利用导数求函数的单调性和单调区间
解题思路
先求定义域,然后在其定义域内判断函数的单调性,并求出单调区间
易错点
分类讨论有重复和遗漏
正确答案
详见解析
解析
(Ⅲ)证明:
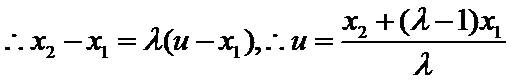
又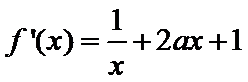
要证: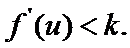
即证: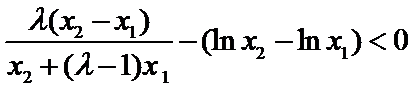
令
令
对称轴
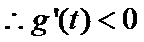
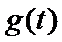
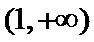
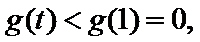

…….12分
考查方向
利用导数证明不等式
构造函数,利用函数的单调性证明不等式
导数、函数、不等式的综合应用
解题思路
先求导,然后根据不等式性质,够造出恰当的函数,然后令其导函数小于K
易错点
构造函数错误,计算能力弱
选修4-1:几何证明选讲
如图所示,AC为⊙O的直径,D为弧BC的中点,E为BC的中点.
28.求证:DE∥AB;
29.求证:ACBC= 2ADCD.
正确答案
详见解析
解析
(Ⅰ)连接

所以
因为


因为

所以
考查方向
圆切线的判定和证明
解题思路
作切线,然后找角的等量关系,然后证明平行
正确答案
详见解析
解析
(Ⅱ)因为

又





所以


考查方向
与圆有关的比例线段,相似三角形的性质和判定
解题思路
先证明三角形DAC和三角形ECD相似,然后得到比例式,进而转换成证明结论