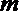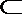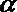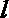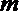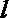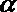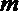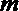- 真题试卷
- 模拟试卷
- 预测试卷
2.设


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.已知等差数列



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
1.已知集合M={0,1,2},N={x|x=2a,a∈M},则集合M∩N等于( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.在△ABC中,“

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.若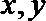
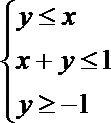
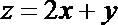
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.设



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.设有一几何体的三视图如下,则该几何体体积为( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.偶函数







正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.设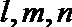
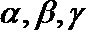
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.实数x满足

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.函数f(x)=
正确答案
[3,+∞)
解析
解析已在路上飞奔,马上就到!
知识点
13.已知定义在R上的函数






正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12.已知数列




正确答案
47
解析
解析已在路上飞奔,马上就到!
知识点
14.若函数f(x)=x2-4x-6的定义域为[0,m],值域为[-10,-6],则m的取值范围是_______。
正确答案
[2,4]
解析
解析已在路上飞奔,马上就到!
知识点
15.下图表示了一个由区间(0,1)到实数集R的映射过程:区间(0,1)中的实数m对应数轴上的点M,如图1;将线段AB围成一个圆,使两端点A.B恰好重合,如图2;再将这个圆放在平面直角坐标系中,使其圆心在y轴上,点A的坐标为(0,1),如图3。对于图3中直线AM与x轴交于点N(n ,0),则 m的象就是n,记作
下列说法中正确的是_______________。(填出所有正确命题的序号)
①
②
③
④

⑤

⑥
⑦
正确答案
①③④
解析
解析已在路上飞奔,马上就到!
知识点
16.已知函数
(1)求函数
(2)求函数
正确答案
(1)增区间

(2)最大值
解析
解析已在路上飞奔,马上就到!
知识点
18.已知数列







(Ⅰ)求数列{
(Ⅱ)若



正确答案
解:(Ⅰ)由已知

则



=
n=1时,
(Ⅱ) 

则

解析
解析已在路上飞奔,马上就到!
知识点
17.设函数


(1)求
(2)求函数
正确答案
解:(1)
所以

解得

(2)因为



所以当

当

所以


解析
解析已在路上飞奔,马上就到!
知识点
20.已知以原点O为中心的椭圆,它的短轴长为



(Ⅰ) 求椭圆的方程和离心率;
(Ⅱ) 若
正确答案
(Ⅰ)解:由题意,可知椭圆的方程为
由已知得
解得
所以椭圆的方程为

(Ⅱ)解:由(1)可得A(3,0).
设直线PQ的方程为y=k(x-3).
联立方程组
依题意△=12(2-3k2)>0,得
设P(x1,y1),Q(x2,y2),则


由直线PQ的方程得为y1=k(x1-3),y2=k(x2-3),
于是,y1y2=k2(x1-3) (x2-3)= k2[x1x2-3(x1+ x2)+9]. 、 ③
∵
由①②③④得5k2=1,从而
所以直线PQ的方程为

解析
解析已在路上飞奔,马上就到!
知识点
21.已知函数

(1)求实数
(2)若关于


(3)证明:对任意的正整数n,不等式
正确答案
(3)略
解析
解析已在路上飞奔,马上就到!
知识点
19.因发生意外交通事故,一辆货车上的某种液体泄露到一鱼塘中。为治理污染,根据环保部门的建议,现决定在鱼塘中投放一种可与污染液体发生化学反应的药剂。已知每投放



(1)若一次投放4个单位的药剂,则有效治污的时间可达几天?
(2)若因材料紧张,第一次只能投放2个单位的药剂,6天后再投放


正确答案
解:(1)因为 

①当



②当



综合得,
(2) 当


由题意知,

因为


故当且仅当


令



又

解析
解析已在路上飞奔,马上就到!