- 真题试卷
- 模拟试卷
- 预测试卷
1.已知集合


正确答案
解析
由
知识点
4.命题“任意x∈[1,2],x2-a≤0”为真命题的一个充分不必要条件是( )
正确答案
解析
命题“任意x∈[1,2],x2-a≤0”为真命题的充要条件是a≥4.故其充分不必要条件是集合[4,+∞)的真子集,正确选项为C
知识点
7.动圆C经过点F(1,0),并且与直线x=-1相切,若动圆C与直线y=x+2+1总有公共点,则圆C的面积( )
正确答案
解析
设圆心C(a,b),半径为r,r=|CF|=|a+1|,即(a-1)2+b2=(a+1)2,即







知识点
6.函数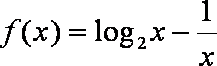
正确答案
解析
∵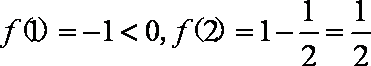
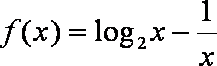
知识点
2.下列函数中,既是偶函数又在区间(0,+ ∞)上单调递减的是( )
正确答案
解析




知识点
8.对向量a=(a1,a2),b=(b1,b2)定义一种运算“⊗”:a⊗b=(a1,a2)⊗(b1,b2)=(a1b1,a2b2).已知动点P,Q分别在曲线y=sin x和y=f(x)上运动,且



正确答案
解析
设P=(x1,y1),Q=(x,y),∵m=(
∴m⊗


∵


∴
∴

又y1=sin x1,∴

∴y=3sin(2x-

知识点
3.已知点M(5,-6)和向量a=(1,-2),若
正确答案
解析
选A 



知识点
5.某程序框图如图所示,若输出的S=120,则判断框内为( )
正确答案
解析
依题意,进行第一次循环时,k=1+1=2,S=2×1+2=4;进行第二次循环时,k=2+1=3,S=2×4+3=11;进行第三次循环时,k=3+1=4,S=2×11+4=26;进行第四次循环时,k=4+1=5,S=2×26+5=57;进行第五次循环时,k=5+1=6,S=2×57+6=120,此时结束循环,因此判断框内应为“k>5?”,选B.
知识点
10.已知双曲线

正确答案

解析
∵双曲线的一个焦点在直线l上,
令y=0,可得x=5,即焦点坐标为(5,0),∴c=5,
∵双曲线

∴
∴双曲线的方程为

知识点
9.复数
正确答案
解析



知识点
14.一个平面图由若干顶点与边组成,各顶点用一串从1开始的连续自然数进行编号,记各边的编号为它的两个端点的编号差的绝对值,若各条边的编号正好也是一串从1开始的连续自然数,则称这样的图形为“优美图”.已知如图是“优美图”,则点A,B与边a所对应的三个数分别为________.
正确答案
3、6、3
解析
观察图中编号为4的边,由于6-2=5-1=4,而数字2已为一端点的编号,故编号为4的边的左、右两端点应为5、1,从而易知编号为1的边的左、右两端点应为4、3.考虑到图中编号为1的边,易知点A对应的数为3,点B对应的数为6.故应填3、6、3.
知识点
11.一个几何体的三视图如图所示,则该几何体的体积是()
正确答案
12
解析
该几何体是两个全等的斜四棱柱对接而成的几何体,其中每个四棱柱是底面邻边长分别为3, 2的长方形,高为1,所以该几何体的体积为:
知识点
13.若x,y满足约束条件
正确答案
-3
解析
作出不等式组
知识点
12.在△ABC中,角




正确答案
解析
由题意有



知识点
16.(本题满分13分)已知函数f(x)=(2cos2x-1)sin 2x+
(1)求f(x)的最小正周期和最大值;
(2)当

正确答案
见解析。
解析
(1)因为f(x)=(2cos2x-1)sin 2x+
=cos 2xsin 2x+

=
所以f(x)的最小正周期为

(2)因为f(α)=

因为

所以

知识点
19.已知椭圆



(1)求椭圆的方程;
(2)过点M(0,-1)作直线l交椭圆于A,B两点,交x轴于N点,且满足

正确答案
见解析。
解析
(1)设椭圆的右焦点为(c,0)(c>0),则



又离心率

故a=2


故椭圆的方程为
(2)设A(x1,y1),B(x2,y2),N(x0,0),因为

所以(x1-x0,y1)=-

易知当直线l的斜率不存在或斜率为0时,①不成立,
于是设直线l的方程为y=kx-1(k≠0),
联立方程
消去x得(4k2+1)y2+2y+1-8k2=0,②
因为Δ>0,所以直线与椭圆相交,
于是y1+y2=-
y1y2=
由①③得,
代入④整理得8k4+k2-9=0,k2=1,k=±1,
所以直线l的方程是y=x-1或y=-x-1.
知识点
20.设函数f(x)=
(1)求b,c的值;
(2)若a>0,求函数f(x)的单调区间;
(3)设函数g(x)=f(x)+2x,且g(x)在区间(-2,-1)内存在单调递减区间,求实数a的取值范围.
正确答案
见解析。
解析
(1)函数的定义域为(-∞,+∞),f′(x)=x2-ax+b,
由题意得
(2)由(1)得,f′(x)=x2-ax=x(x-a)(a>0),
当x∈(-∞,0)时,f′(x)>0,当x∈(0,a)时,f′(x)<0,
当x∈(a,+∞)时,f′(x)>0.
所以函数f(x)的单调递增区间为(-∞,0),(a,+∞),单调递减区间为(0,a).
(3)g′(x)=x2-ax+2,
依题意,存在x∈(-2,-1),使不等式g′(x)=x2-ax+2<0成立,
即x∈(-2,-1)时,
当且仅当“x=

所以满足要求的a的取值范围是(-∞,-2
知识点
15.(本题满分13分)已知公差大于零的等差数列{an}的前n项和为Sn,且满足a3·a4=117,a2+a5=22.
(1)求an和Sn;
(2)若数列{bn}是等差数列,且bn=
正确答案
见解析。
解析
(1)∵数列{an}为等差数列,∴a3+a4=a2+a5=22.
又a3·a4=117,
∴a3,a4是方程x2-22x+117=0的两实根,
又公差d>0,∴a3<a4,∴a3=9,a4=13,
∴
∴通项公式an=4n-3.
∴Sn=na1+
(2)由(1)知Sn=2n2-n,∴
∴
∵数列{bn}是等差数列,∴2b2=b1+b3,
即
∴c=-

知识点
17.如图,已知PA⊥平面ABCD,且四边形ABCD为矩形,M,N分别是AB,PC的中点.
(1)求证:MN⊥CD;
(2)若∠PDA=45°,求证:MN⊥平面PCD.
正确答案
见解析。
解析
(1)
如图所示,取PD的中点E,连接AE,NE,
∵N是PC的中点,E为PD的中点,
∴NE∥CD,且NE=
而AM∥CD,且AM=

∴NE綊AM,
∴四边形AMNE为平行四边形,
∴MN∥AE.
又PA⊥平面ABCD,∴PA⊥CD,
又∵ABCD为矩形,∴AD⊥CD.
而AD∩PA=A,∴CD⊥平面PAD,
∴CD⊥AE.又AE∥MN,∴MN⊥CD.
(2)∵PA⊥平面ABCD,∴PA⊥AD,
又∠PDA=45°,
∴△PAD为等腰直角三角形.
又E为PD的中点,
∴AE⊥PD,又由(1)知CD⊥AE,PD∩CD=D,
∴AE⊥平面PCD.
又AE∥MN,∴MN⊥平面PCD.
知识点
18.交通指数是交通拥堵指数的简称,是综合反映道路网畅通或拥堵的概念,记交通指数为T,其范围为[0,10],分别有五个级别:T∈[0,2)畅通;T∈[2,4)基本畅通;T∈[4,6)轻度拥堵;T∈[6,8)中度拥堵;T∈[8,10]严重拥堵.晚高峰时段(T≥2),从某市交通指挥中心选取了市区20个交通路段,依据其交通指数数据绘制的部分直方图如图所示.
(1)请补全直方图,并求出轻度拥堵、中度拥堵、严重拥堵路段各有多少个;
(2)用分层抽样的方法从交通指数在[4,6),[6,8),[8,10]的路段中共抽取6个路段,求依次抽取的三个级别路段的个数;
(3)从(2)中抽出的6个路段中任取2个,求至少1个路段为轻度拥堵的概率.
正确答案
见解析。
解析
(1)补全直方图如图:
由直方图可知:(0.1+0.2)×1×20=6,
(0.25+0.2)×1×20=9,
(0.1+0.05)×1×20=3.
∴这20个路段中,轻度拥堵、中度拥堵、严重拥堵的路段分别为6个、9个、3个.
(2)由(1)知拥堵路段共有6+9+3=18个,按分层抽样从18个路段中选出6个,每种情况分别为:


(3)记(2)中选取的2个轻度拥堵路段为A1,A2,选取的3个中度拥堵路段为B1,B2,B3,选取的1个严重拥堵路段为C1,
则从6个路段选取2个路段的可能情况如下:
(A1,A2),(A1,B1),(A1,B2),(A1,B3),(A1,C1),(A2,B1),(A2,B2),(A2,B3),(A2,C1),(B1,B2),(B1,B3),(B1,C1),(B2,B3),(B2,C1),(B3,C1),共15种可能.
其中至少有1个轻度拥堵的有:(A1,A2),(A1,B1),(A1,B2),(A1,B3),(A1,C1),(A2,B1),(A2,B2),(A2,B3),(A2,C1),共9种可能.
∴所选2个路段中至少1个路段轻度拥堵的概率为























