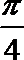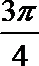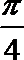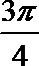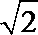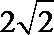- 真题试卷
- 模拟试卷
- 预测试卷
2.定义




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.已知公差不为0的等差数列



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.对某种电子元件使用寿命跟踪调查,抽取容量为1000的样本,其步率分布直方图如图所示,根据此图可知这样样本中电子元件的寿命在300-500小时的数量是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.下列命题错误的是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.已知向量

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.函数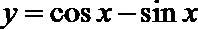
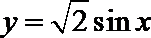
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
1.设

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.正数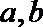
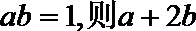
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.若函数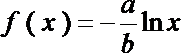
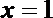
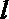
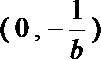
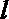
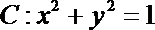
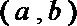
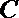
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.设F1、F2是双曲线

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
13.在海岛A上有一座海拔1千米的山,山顶上有一个观察站P,上午11时,测得一轮船在岛的北偏东30°,俯角30°的B处,到11时10分又测得该船在岛的北偏西60°,俯角60°的C处,则轮船航行速度是__________千米/小时。
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15.已知




正确答案
41
解析
解析已在路上飞奔,马上就到!
知识点
11.某服装加工厂某月生产A、B、C三种产品共4000件,为了保证产品质量,进行抽样检验,根据分层抽样的结果,企业统计员制作了如下的统计表格:
由于不小心,表格中A、C产品
正确答案
800
解析
解析已在路上飞奔,马上就到!
知识点
12.已知


正确答案
-6
解析
解析已在路上飞奔,马上就到!
知识点
14.按下图所示的程序框图运算,若输出

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
20.已知首项不为零的数列





(Ⅰ)判断数列
(Ⅱ)若数列










正确答案
(Ⅰ)令



当

当

综上知,
所以
故数列

(Ⅱ)当

于是

因此数列




故
解析
解析已在路上飞奔,马上就到!
知识点
18.一个多面体的三视图和直观图如图所示,其中正视图和俯视图均为矩形,侧视图为直角三角形, M、G分别是AB、DF的中点。
(1)求证:CM
(2)在线段AD上确定一点P,使得GP//平面FMC,并给出证明;
正确答案
解:
由三视图可得直观图为直三棱柱且底面ADF中
(1)显然
又
在矩形ABCD中,
M为AB中点,




(2)点P在A点处,
证明:取DC中点S,连接AS、GS、GA


而

解析
解析已在路上飞奔,马上就到!
知识点
21. 如图6所示,在直角坐标平面上的矩形











(Ⅰ)求点
(Ⅱ)若过点




正确答案
解 :
(Ⅰ)设点





由


由


于是,当


直线

①


当







(Ⅱ)设过点




由

由于上述方程的判别式
所以

根据求根公式,可得
又


令

于是

记


因为当



故当





综上所述,当




解析
解析已在路上飞奔,马上就到!
知识点
17. 甲,乙两人进行射击比赛,每人射击
(Ⅰ)根据上表中的数据,判断甲,乙两人谁发挥较稳定;
(Ⅱ)把甲6次射击命中的环数看成一个总体,用简单随机抽样方法从中抽取两次命中的环数组成一个样本,求该样本平均数与总体平均数之差的绝对值不超过
正确答案
解 :(Ⅰ)甲射击命中的环数的平均数为
其方差为
乙射击命中的环数的平均数为
其方差为
因此
故甲,乙两人射击命中的环数的平均数相同,但甲比乙发挥较稳定.
(Ⅱ)由(Ⅰ)知,
设

从总体中抽取两个个体的全部可能的结果



其中事件



故所求的概率为
解析
解析已在路上飞奔,马上就到!
知识点
19. 已知:
(1)设

(2)若

正确答案
解:(1)
又
由
由
得

(2)由(1)知
先考虑
则




得:


解析
解析已在路上飞奔,马上就到!
知识点
16.在
(1)求
(2)设D为AC中点,求
正确答案
解:由题意得

(1)
(2)
解析
解析已在路上飞奔,马上就到!