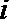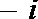- 真题试卷
- 模拟试卷
- 预测试卷
1.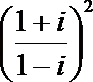
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.已知某生产厂家的年利润


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.设




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.命题“
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.已知

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.已知函数


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.已知函数

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.下面的三段论推理“菱形是平行四边形;四边形ABCD是平行四边形;所以四边形ABCD是菱形”结论显然是错误的,其错误的原因是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2.已知集合



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.计算机执行下面的程序后,输出的结果是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.函数



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12.若曲线y=ax2-lnx在点


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
13.函数

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15.已知函数


①若


②


③函数


④



⑤



其中正确命题的序号为_____.
正确答案
①②③④
解析
解析已在路上飞奔,马上就到!
知识点
14.一个几何体的三视图如图所示,则其体积为________.
正确答案
4
解析
解析已在路上飞奔,马上就到!
知识点
18.为了了解我市工厂开展文明创建活动的情况,拟采用分层抽样的方法从相山区、杜集区、烈山区中抽取7个单位进行调查.已知相山区、杜集区、烈山区中分别有18、27、18个工厂.
(1)求相山区、杜集区、烈山区中应分别抽取的工厂个数;
(2)若从抽得的7个工厂中随机的抽取2个进行调查结果的对比,用列举法计算这2个工厂中至少有一个来自相山区的概率。
正确答案
(1)相山区、杜集区、烈山区中应分别抽取的工厂个数为2个,3个,2个
(2)这2个工厂中至少有一个来自相山区的概率为
解析
解析已在路上飞奔,马上就到!
知识点
16.已知





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
21.已知



(1)求
(2)求证:
(3)求
正确答案
(1)
由题意可得:x=0为f(x)的极值点,
∴
(2)令
∵f(x)在(—∞,0)上是增函数,在[0,2]上是减函数,
∴
又∵
∴
(3)∵方程f(x)=0有三个根α、2、β.
∴设
由待定系数法得
∴α、β为方程
∴ α+β=-(b+2),αβ=-d/2;
∴|α-β|
∵

∴|α-β| ≥3
解析
解析已在路上飞奔,马上就到!
知识点
17.已知向量


(1)求
(2)在三角形ABC中,边





正确答案
(1)
(2)
解析
解析已在路上飞奔,马上就到!
知识点
19.如图,四棱锥E—ABCD中,底面ABCD为矩形,平面ABE⊥平面ABCD,AE⊥EB,AC与BD交于M,BE=BC,F为CE的中点。
(I)求证:AE//平面BDF;
(II)求证:BF⊥平面ACE。
正确答案
证明:(1)设AC∩BD=G,连接FG,易知G是AC的中点,
∵F是EC中点,由三角形中位线的性质可得 FG∥AE,
∵AE⊄平面BFD,FG⊂平面BFD,∴AE∥平面BFD.
(2)∵平面ABCD⊥平面ABE,BC⊥AB,
平面ABCD∩平面ABE=AB∴BC⊥平面ABE,
又∵AE⊂平面ABE,∴BC⊥AE,
又∵AE⊥BE,BC∩BE=B,∴AE⊥平面BCE,∴AE⊥BF.
在△BCE中,BE=CB,F为CE的中点,
∴BF⊥CE,AE∩CE=E,∴BF⊥平面ACE,
又BF⊂平面BDF,∴平面BDF⊥平面ACE,∴BF⊥平面ACE.
解析
解析已在路上飞奔,马上就到!
知识点
20.现有一张长为80cm,宽为60cm的长方形铁皮ABCD,准备用它做成一只无盖长方体铁皮盒,要求材料利用率为100%,不考虑焊接处损失。如图,若长方形ABCD的一个角剪下一块正方形铁皮,作为铁皮盒的底面,用余下材料剪拼后作为铁皮盒的侧面,设长方体的底面边长为x (cm),高为y (cm),体积为V (cm3)
(1)求出x 与 y 的关系式;
(2) 求该铁皮盒体积V的最大值。
正确答案
解:(1)由题意得
即

(2)铁皮盒体积



因为





所以


答:该铁皮盒体积

解析
解析已在路上飞奔,马上就到!