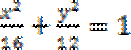- 真题试卷
- 模拟试卷
- 预测试卷
2.已知复数


正确答案
解析
本题考查了复数的乘除运算与复数的求模这些知识点.两边同时除以1+i,则z=

考查方向
本题主要考查复数的乘除运算与复数求模这些知识点,在各省高考题出现的频率非常高,属于基础题,体现了学生对基础知识的掌握能力。
易错点
本题易在使用i2=-1时发生错误.
知识点
3.下列有关命题的说法中,正确的是( )
正确答案
解析
1、无论x0是R中的什么数,3x0总大于0,所以A选项不正确;
2、当0<x<1时,lgx<0,B选项不正确;
3、由




4、D正确。
考查方向
本题主要考查了命题的真假性与充要条件的判断这个知识点,常与各种知识揉合在一起,但难度不大,属于基础题。
易错点
1、本题易混淆“



2、对“必要不充分”与“充分不必要”理解不透.
知识点
4.过点



正确答案
解析
本题考查了利用截距式求直线方程这个知识点分两种情况:①当截距不为0时,设在x轴上的截距为a,则在y轴上的截距为2a,所以直线方程为

考查方向
本题主要考查了求直线方程这个知识点,是高考C级考点之一,几乎是高考必考内容,属于基础题,体现了学生对基础知识的掌握情况.求直线方程通常有下面几种方法:
①点斜式;②斜截式;③两点式;④截距式;⑤一般式。
易错点
本题易忽视截距为0这种情况,导致少一个答案 .
知识点
7. 若椭圆




正确答案
解析
由椭圆和双曲线的定义,得


考查方向
本题主要考查了椭圆和双曲线的定义。
易错点
本题易在利用双曲线定义得到
知识点
8.若点




正确答案
解析
设














考查方向
本题主要考查了简单的线性规划。
易错点
本题易在画可行域和目标函数基准直线时出现错误,易忽视“目标函数基准线与可行域边界的倾斜程度”.
知识点
10.已知直线


正确答案
解析
由题意,得





考查方向
本题主要考查了直线与圆的位置关系,在近几年的各省高考题中出现的频率较高,常与三角形、点到直线的距离等知识交汇命题。
易错点
本题易在由



知识点
1.已知集合
正确答案
解析
本题考查了一元二次不等式的解法、对数函数定义域求法、集合的交集与补集运算.解不等式x2-x-2<0,得-1<x<2,所以A=(-1,2),又因为1-|x|>0,解得-1<x<1,所以B=(-1,1),所以


考查方向
本题主要考查了集合的交集与补集运算,是基础题,是高考必考题型之一,常与求不等式的解集,函数的定义域、值域等知识点交汇命题,体现了学生对基础知识的掌握能力。
易错点
本题易在求对数函数的定义域中发生错误.
知识点
5. 已知



正确答案
解析
本题主要考查了三角函数的图象与性质。因为f(x)=sinx的单调减区间是[2k






考查方向
本题主要考查了三角函数的图象与性质,属于中档题,是高考热点之一,常与三角化简、恒等变形公式,函数单调性、周期性、对称型、奇偶性等知识点交汇命题。
易错点
本题易在f(x)=sinx的增减区间上发生错误,f(x)=sinx的单调增区间是[2k




知识点
6.抛物线





正确答案
解析
因为抛物线











考查方向
本题主要考查了抛物线的定义的应用。
易错点
本题易在将抛物线上的点到直线

知识点
9.已知



正确答案
解析
因为








考查方向
本题主要考查了函数的单调性和比较大小。
易错点
本题易在判定
知识点
11.已知函数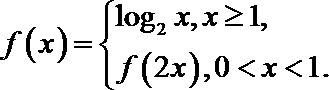
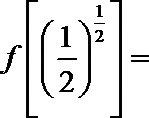
正确答案
解析
因为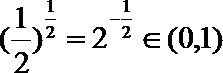
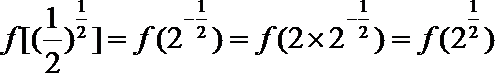

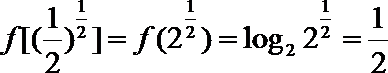
考查方向
本题主要考查了分段函数的求值、对数的运算。
易错点
本题易在判定
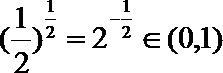
知识点
12.已知偶函数






正确答案
解析
由










考查方向
本题主要考查了函数的性质(奇偶性、周期性)和方程的根的个数。
易错点
本题易在时由

知识点
15.已知P是抛物线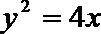
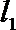
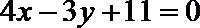
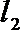
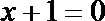
正确答案
3
解析
过点P作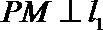
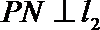
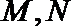
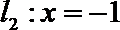
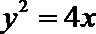
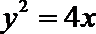
由抛物线的定义,得|PN|=|PF|,过点P作直线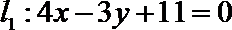
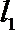
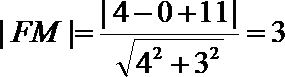
所以P到直线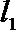
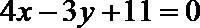
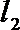
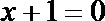
考查方向
本题主要考查了抛物线的定义和标准方程。
易错点
本题易在得到|PN|=|PF|时出现错误,易忽视“利用抛物线的定义将抛物线上的点到准线的距离转化为到焦点的距离”的应用.
知识点
16. 对于下列命题:其中所有真命题的序号是 ____ .
① 函数


②已知



③“


④“

⑤
正确答案
①②④
解析
①因为函数







②已知



③由绝对值的几何意义,得



④“方程


⑤因为

所以答案为①②④。
考查方向
本题主要考查了充分条件和必要条件的判定以及命题真假的判定,在近几年的各省高考题中出现的频率较高,常与集合的关系、函数的定义域、性质、不等式的解集等知识交汇命题。
易错点
本题易在判定②时出现错误,易忽视“直线

知识点
18.如图,在四棱锥


(I)求证:平面
(II)求三棱锥
正确答案
(1)见解析;
(2)
解析
本题属于立体几何应用中的基本问题,题目的难度不大,用到一些平面几何的知识。
(1)化为求线面垂直
(2)转变思想,换个角度看问题。
(I)连接BQ,因为ABCD是直角梯形,AD∥BC,AD=2BC,Q为AD的中点,
所以BCDQ为平行四边形,又因为CD=

因为ΔPAD是边长为2的正三角形,Q是AD的中点,
所以PQ⊥AD,PQ=
在ΔPQB中,QB=


因为AD∩BQ=Q,AD、BQ
所以PQ⊥平面ABCD.
因为PQ
(II)由(I)知:PQ⊥平面ABCD,PQ=
因为底面ABCD为直角梯形,AD∥BC,∠ADC=
所以ΔBCD是直角三角形,其中∠BCD=
因为BC=1,CD=

考查方向
本题考查了空间面面垂直、求椎体体积等知识,全面考查了学生阅读能力、空间想象能力与分析问题解决问题的能力,属于中档题,立体几何也是高考的必考内容,常与平几知识相结合,也有的会需要建立空间坐标系,结合空间向量的知识解决。
易错点
第二问求三棱锥的体积,如果不知道转化,则无法求出.
知识点
19.已知曲线Γ上的点到



(1)求曲线Γ的方程;
(2)若

(3)设点





正确答案
(1)曲线Γ的方程为
(2)
(3)
解析
本题综合性较强,题目有一定难度,需要透彻理解抛物线的定义,巧设直线方程,灵活运用一元二次方程根与系数的关系来求。
解:(1)因为点到




(2)设A(x1,y1),B(x2,y2)因为直线过F(1,0),所以设lAB:x=my+1,又因为










考查方向
本题是一个综合性很强的题目,考查了抛物线的定义,直线的斜率、向量的坐标式、一元二次方程根与系数关系等知识,在抛物线、向量、方程根等处进行了交汇,有一点的难度,考查了学生对基础知识的掌握能力、综合运用能力。
易错点
第二问中设直线方程为x=my+1,可以使解题方便,若设y=k(x-1),需要考虑斜率不存在的情况.
知识点
20.已知椭圆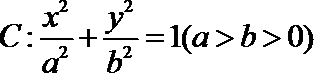
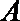
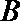
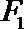
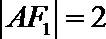
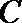
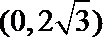
(Ⅰ)求椭圆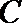
(Ⅱ)点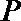
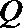
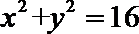
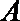
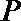
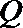
正确答案
(1)椭圆C的方程为
(2)见解析
解析
本题属于直线与椭圆关系的基本问题,题目的难度是逐渐由易到难,
(1)根据题目条件和a、b、c的关系可求
(2)设出两个交点的坐标
(3)根据已知条件,求出斜率关系,最后得出结论。
解:(I)由已知可得a-c=2,b=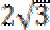
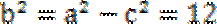
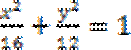
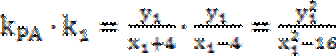
因为P(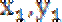
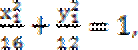
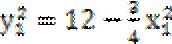
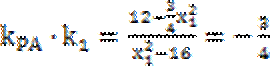
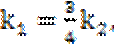
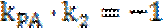
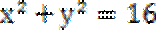
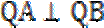
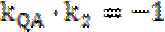
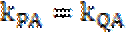
考查方向
本题考查了椭圆的基本性质以及直线与椭圆的位置关系等知识点,考查了学生分析问题与思考问题的能力,直线与圆锥曲线(特别是椭圆)的关系,是高考的重点内容,涉及的知识点较多,运算也比较复杂,对学生的运算能力有较高的要求,有时会与向量、距离、基本不等式、一元二次方程根与系数关系交汇在一起。
易错点
1、椭圆中a、b、c的关系会与双曲线中的搞错
2、第二问证三点共线,通常是证有公共点的两条直线的斜率相等(或者是采用向量的方法)
知识点
13.已知双曲线

正确答案
解析
本题考查抛物线的焦点坐标,双曲线的离心率、焦点坐标、渐近线方程等知识。
解:因为抛物线为



考查方向
本题主要考查了抛物线的焦点坐标,双曲线的离心率、焦点坐标、渐近线方程等知识,在各地的高考题中出现的频率较高,属于中档题,考查学生对基础知识的掌握与分析问题的能力。
易错点
双曲线中c2=a2+b2,易与椭圆中a2=b2+c2 搞混.
知识点
14.若点



正确答案
解析
本题主要考查了曲线的切线方程、线线之间的距离等知识点。
解:因为





考查方向
本题主要考查了曲线的切线方程、线线之间的距离等知识点,难度中等,是高考热点之一,考查学生分析问题与转化问题的能力。
易错点
本题必须注意把点线之间的距离转化为两条平行线之间的距离,否则会导致无法求出.
知识点
21.已知函数



(Ⅰ)若



(Ⅱ)设函数




(Ⅲ)令



正确答案
(Ⅰ)
(Ⅱ)
(Ⅲ)
解析
本题属于导数的基本问题,题目的难度是逐渐由易到难,
(1)直接按步骤来求,
(2)要注意分离参数;
(3)要注意讨论
(1)设


因为
且

切线方程为

当




(2)
由题意,得
即方程
令
则
所以






(3)因为

因为
所以




显然,当


则

又因为


由①②,得所求实数
考查方向
【考查方向】本题主要考查了导数的应用,导数的应用主要分以下几类:
1.利用导数的几何意义求切线方程,
2.利用导数研究函数的单调性、极值和最值或零点,
3.利用导数研究不等式恒成立或存在性。
易错点
1.第二问中,易忽视分离参数;
2.第三问中,易忽视“
知识点
17.已知向量





(I)求
(II)求函数
(III)若

正确答案
(1)
(2)增区间[

(3)
解析
本题属于三角函数应用中的基本问题,题目的难度是逐渐由易到难,
(1)直接按照步骤来求,
(2)对函数进行变形,转化成可用已知函数表示的形式,最后代入求值。
解:(I)f(x)=2



























考查方向
本题考查了向量的乘法、正(余)弦的二倍角、函数的单调区间、三角的恒等变形与化简求值等知识点,属于中档题,也是高考必考题型之一。向量的坐标式、向量的平行与垂直、三角函数的单调性、周期性、对称轴等知识常常会结合在一起进行命题。
易错点
1、二倍角的余弦公式中符号搞错
2、第(III)问的变形化简会出错