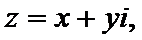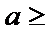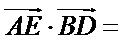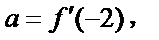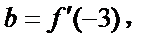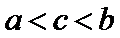- 真题试卷
- 模拟试卷
- 预测试卷
1.设集合

正确答案
解析










考查方向
解题思路
1)解不等式

2)求
易错点
本题易在求集合A的时出现错误,易忽视指数函数的单调性;以及集合B中忘记二次项系数变正.
知识点
2.已知等比数列{an}中,

正确答案
解析




考查方向
解题思路
1)将

2)求
3)将
易错点
本题易在运算上出现错误,也容易按等差数列的性质做题.
知识点
3.在区间



正确答案
解析
因为直线






考查方向
解题思路
1)用圆心到直线的距离小于半径,得到
2)用

易错点
本题易将几何概型当成古典概型去做,只取整数点比较.
知识点
8.已知一个几何体可切割成一个多面体及一个旋转体的一部分,其三视图如图所示,则该几何体的体积是
正确答案
解析
由三视图可得原几何体是由一个半圆柱和一个三棱锥组合而成,圆柱的底面半径为1,高位2,所以体积为


考查方向
解题思路
1)根据几何体的三视图,画出该几何体的直观图;
2)分割几何体,分别判定几何体形状求其体积;
3)求和,即得该几何体的体积。
易错点
本题易在由三视图得到直观图时发生错误,导致体积求错。
知识点
4.设复数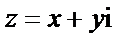
正确答案
解析
因为

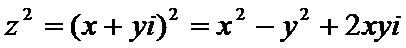

考查方向
解题思路
1)求出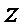
2)分别计算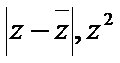
易错点
本题在对


知识点
5.执行两次下图所示的程序框图,若第一次输入的a的值为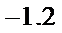
正确答案
解析
当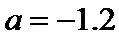
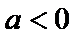


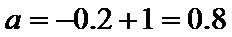
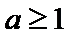
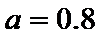
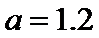

考查方向
解题思路
1)先将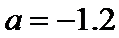
2)再将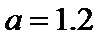
易错点
本题易在验证条件语句时出现错误.
知识点
6.2016年3月9日至15日,谷歌人工智能系统“阿尔法”迎战围棋冠军李世石,最终结果“阿尔法”以总比分4比1战胜李世石.许多人认为这场比赛是人类的胜利,也有许多人持反对意见,有网友为此进行了调查,在参加调查的2548名男性中有1560名持反对意见, 2452名女性中有1200名持反对意见,在运用这些数据说明“性别”对判断“人机大战是人类的胜利”是否有关系时,应采用的统计方法是
正确答案
解析
通过对题意的理解运用这些数据说明“性别”对判断“人机大战是人类的胜利”是否有关系,只有独立性检验可以说明性别与判断“人机大战是人类的胜利”是否有关系,有多大的把握认为他们有关,所以选C选项.
考查方向
解题思路
1.观察答案给的几种情况,分析本题应采用哪一种.
易错点
本题学生们如果对统计中的一些知识点不熟悉的话,可能会选错.
知识点
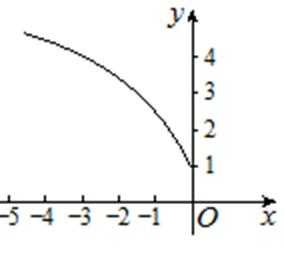
7.下列函数既是奇函数,又在区间
正确答案
解析















考查方向
解题思路
1)分别判断四个选项函数的奇偶性
2)分别判断满足奇函数性质的函数的单调性.
易错点
本题学生们对一些复合函数的性质判断上容易出现错误.
知识点
9.给定两个命题p,q,若

正确答案
解析
若





考查方向
解题思路
1) 若


2)将命题变为它的逆否命题;
3)再判断充分条件和必要条件。
易错点
本题易在用原命题与逆否命题同真假时出现错误。
知识点
10.将所有正偶数按如下方式进行排列,则2 016位于
第1行:2 4
第2行:6 8 10 12
第3行:14 16 18 20 22 24
第4行:26 28 30 32 34 36 38 40
…… …… ……
正确答案
解析
因为2016是第1008个偶数,按照题意进行排列,得到一个新的等差数列,





考查方向
解题思路
1)计算2016是第几个正偶数;
2)求新的等差数列的通项公式;
3)找出2016在第几行.
易错点
本题易在运算上出现错误,也容易在项数上出现错误。
知识点
11.已知四棱锥







正确答案
解析
由题意可得直观图如图所示,
因为






考查方向
解题思路
1)由已知条件画出草图;
2)找到球心的位置,以及构造直角三角形;
3)在直角三角形中计算球的半径,以及表面积.
易错点
本题由题意画出立体几何的图是一个难点,将立体的计算转化为平面也是难点。
知识点
12.已知集合

正确答案
解析
因为集合



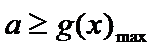
令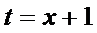
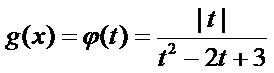
①当
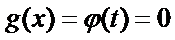
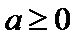
②当
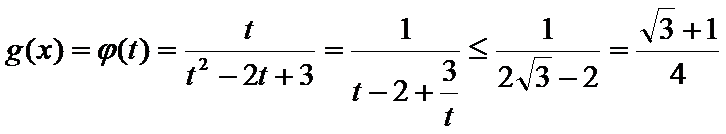

③当

∴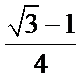
综上,取交集得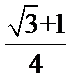
考查方向
解题思路
1)将恒成立问题转化为求最值;
2)对

易错点
本题恒成立转化为求最值时较难,分离参数后用对勾函数的性质时忘记讨论
知识点
13.若实数x,y满足
正确答案
1
解析
将


当直线





考查方向
解题思路
1)作出


2)由图象判定最优解与最优点;
3)再代入z=3x+2y.
易错点
本题易在求目标函数的最值时出现问题,注意目标函数的斜率与区域边界线的斜率比较
知识点
14.已知正方形ABCD的边长为2,E为CD的中点,则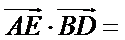
正确答案
2
解析
因为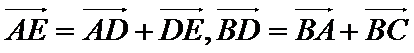
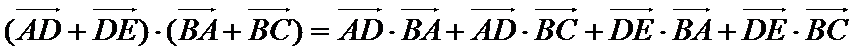
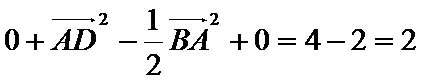
考查方向
解题思路
1)利用向量的加减法将已知向量转化为共线向量;
2)用向量数量积的定义计算。
易错点
本题易在用向量的加减法将向量转化为共线的向量时出现错误。
知识点
15.函数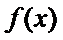
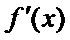
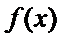
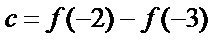
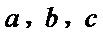
正确答案
解析
由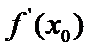
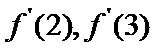
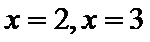
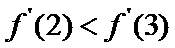
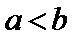
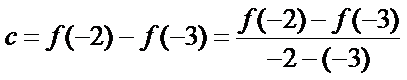
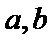
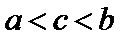
考查方向
解题思路
1)由导函数的几何意义,将导函数转化为切线斜率;
2)由导函数的定义将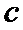
易错点
本题易将导函数图像与原函数图像弄错,容易忘记导函数的定义;
知识点
16.已知数列{an}满足a1


正确答案
解析
易知=+1,∴+1=2(+1).
又a1=1,∴+1=(+1)

当

∴bn+1-bn=(n-λ)2n-(n-1-λ)

又n∈N*,∴λ<2.
考查方向
解题思路
1)由

2)由数列单调性的定义求
易错点
本题易根据函数的单调性判断数列的单调性,忽略数列自变量的特殊性;
知识点
已知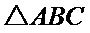
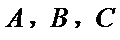
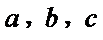
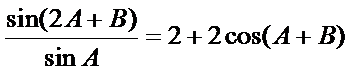
17.求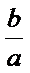
18.若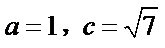
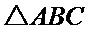
正确答案
(1)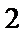
解析
(Ⅰ)∵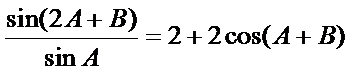
∴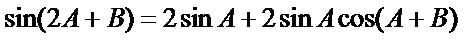
∴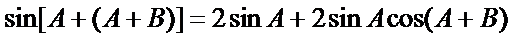
∴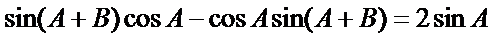
∴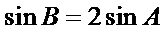
∴
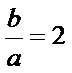
考查方向
解题思路
1)第一问中用两角和差公式和三角恒等变换化简得到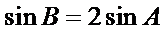
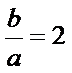
2)第二问中用倍余弦定理得到一个角,在用三角形面积公式求得面积。
易错点
1)第一问中想不到将角
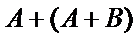
2)第二问中用余弦定理求角时容易将特殊角记错。
正确答案
(2)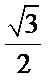
解析
(Ⅱ)∵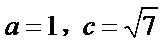
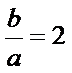
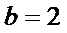
∴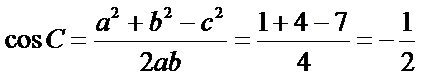
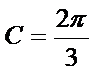
∴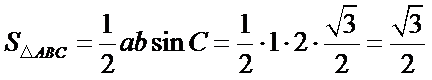
即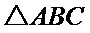
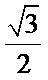
考查方向
解题思路
1)第一问中用两角和差公式和三角恒等变换化简得到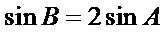
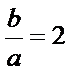
2)第二问中用倍余弦定理得到一个角,在用三角形面积公式求得面积。
易错点
1)第一问中想不到将角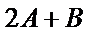
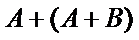
2)第二问中用余弦定理求角时容易将特殊角记错。
已知某中学高三文科班学生共有



(Ⅰ)如果从第




(Ⅱ)抽的
21.成绩分为优秀、良好、及格三个等级,横向、纵向分别表示地理成绩与数学成绩,例如:表中数学成绩为良好的共有


22.将



正确答案
(1)

解析
(Ⅰ)依题意,最先检测的3个人的编号依次为
(Ⅱ)由

因为

考查方向
解题思路
1)第一问考察统计的知识,比较简单,直接由比例可得出
2)第二问中属于古典概型,较简单,直接列举出所有的情况,数出个数作商。
易错点
容易在找出满足条件的所有事件时丢掉。
正确答案
(2)
解析
(Ⅲ)由题意,知

故满足条件的



其中数学成绩为优秀的人数比及格的人数少有:


∴数学成绩优秀的人数比及格的人数少的概率为
考查方向
解题思路
1)第一问考察统计的知识,比较简单,直接由比例可得出
2)第二问中属于古典概型,较简单,直接列举出所有的情况,数出个数作商。
易错点
容易在找出满足条件的所有事件时丢掉。
已知点











23.当点



24.过点











正确答案
(1)
解析
(Ⅰ)设点





由

由



则由




考查方向
解题思路
1)第一问利用向量垂直的充要条件,以及


2)第二问首先设出





易错点
计算量大,未知数比较多,计算上出错。
正确答案
(2)
解析
(Ⅱ)由题意知直线


联立


∴





∴
∴
∴
∵

∴


考查方向
解题思路
1)第一问利用向量垂直的充要条件,以及


2)第二问首先设出





易错点
计算量大,未知数比较多,计算上出错。
如图,直三棱柱ABC
19.证明:平面AEF⊥平面B1BCC1;
20.若直线A1C与平面A1ABB1所成的角为45°,求三棱锥F
正确答案
(1)略;
解析
(Ⅰ)证明:如图,因为三棱柱ABC A1B1C1是直三
又E是正三角形ABC的边BC的中点,所以AE⊥BC.
又
而AE⊂平面AEF,所以平面AEF⊥平面B1BCC1.
考查方向
解题思路
1)第一问通过等边三角形的性质找到AE⊥BC,再由线面垂直的判定得到线面垂直,最后得到面面垂直;
2)第二问先找到直线A1C与平面A1ABB1所成的角,通过线面角求得A1D=CD=
易错点
证明面面垂直找不到线面垂直的条件,由已知的线面角找不出长度的关系。
正确答案
(2)
解析
(Ⅱ)设AB的中点为D,连接A1D,CD.
因为△ABC是正三角形,所以CD⊥AB.
又三棱柱ABC A1B1C1是直三棱柱,所以CD⊥AA1.
又
于是∠CA1D为直线A1C与平面A1ABB1所成的角.
由题设,∠CA1D=45°,所以A1D=CD=
在Rt△AA1D中,AA1=
故三棱锥F 
考查方向
解题思路
1)第一问通过等边三角形的性质找到AE⊥BC,再由线面垂直的判定得到线面垂直,最后得到面面垂直;
2)第二问先找到直线A1C与平面A1ABB1所成的角,通过线面角求得A1D=CD=
易错点
证明面面垂直找不到线面垂直的条件,由已知的线面角找不出长度的关系。
已知函数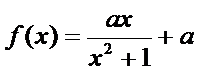

25.求函数f (x)的单调区间;
26.证明:当a > 0时,对于任意x1,x2∈(0,e],总有g(x1) < f (x2)成立,其中
正确答案
(1)当a>0时,f (x)的单调递增区间为(-1,1),单调递减区间为(-∞,-1),(1,+∞);
当a<0时,f (x)的单调递增区间为(-∞,-1),(1,+∞),单调递减区间为(-1,1);
解析
(Ⅰ)函数f (x)的定义域为R,f ′(x)=
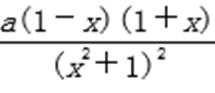
当a>0时,当x变化时,f ′(x),f(x)的变化情况如下表:
当a<0时,当x变化时,f ′(x),f(x)的变化情况如下表:
综上所述,
当a>0时,f (x)的单调递增区间为(-1,1),单调递减区间为(-∞,-1),(1,+∞);
当a<0时,f (x)的单调递增区间为(-∞,-1),(1,+∞),单调递减区间为(-1,1).
考查方向
解题思路
1)第一问对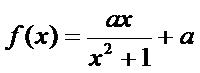
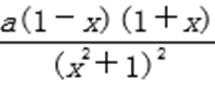
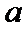
2)第二问由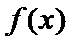
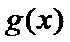
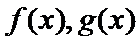
正确答案
(2)略;
解析
(Ⅱ)由(Ⅰ)可知,当a>0时,f (x)在区间(0,1)上单调递增,f (x)
f (x)在区间(1,e]上单调递减,且f (e)=
因为g(x)=aln x-x,所以g′(

①当a≥e时,g′(x)≥0在区间(0,e]上恒成立,
所以函数g(x)在区间(0,e]上单调递增,所以g(x)max=g(e)=a-e<a.
所以对于任意x1,x2∈(0,e],仍有g(x1)<f(x2).
②当0<a
因为a-(aln a-a)=a(2-ln a)>a(2-ln e)=a>0,
所以对任意x1,x2∈(0,e],总有g(x1)<f (x2).
综上所述,对于任意x1,x2∈(0,e],总有g(x1)<f (x2).
考查方向
解题思路
1)第一问对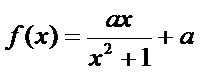
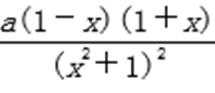

2)第二问由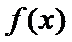
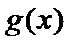
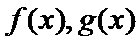
选修4-1:几何证明选讲
如图,过圆













27.求
28.求
正确答案
(1)3;
解析
(Ⅰ)延长




又

又


根据切割线定理得

考查方向
解题思路
1)第一问由切割线定理可得;
2)第二问将两条线段归到两个相似三角形中,用相似得到比例关系。
易错点
三角形相似容易找错,切割线定理用不熟练。
正确答案
(2)
解析
(Ⅱ)过




又由题意知

因此
考查方向
解题思路
1)第一问由切割线定理可得;
2)第二问将两条线段归到两个相似三角形中,用相似得到比例关系。
易错点
三角形相似容易找错,切割线定理用不熟练。