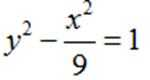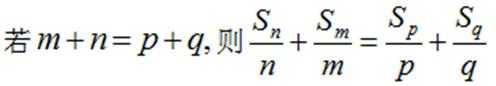文科数学黄浦区2012年高三试卷

精品

填空题
单选题
简答题

立即下载

文科数学热门试卷

X 查看更多试卷

试卷目录

1、填空题

2、单选题

3、简答题

真题试卷
模拟试卷
预测试卷

填空题本大题共14小题，每小题4分，共56分。把答案填写在题中横线上。

题型：填空题

分值: 4分

2．已知是纯虚数，则_________．

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

指数函数的图像变换

题型：填空题

分值: 4分

7．函数的部分图像如图所示，则_________．

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

求函数y＝Asin(ωx＋φ)的解析式

题型：填空题

分值: 4分

9．若数列满足（为常数），则称数列为等比和数列，称为公比和．已知数列是以3为公比和的等比和数列，其中，则_________．

正确答案

21006

解析

解析已在路上飞奔，马上就到！

知识点

幂函数的概念、解析式、定义域、值域

题型：填空题

分值: 4分

10．设函数的图像过点，其反函数的图像过点，则等于_________ ．

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

指数函数的图像变换

题型：填空题

分值: 4分

1．若，则是的_________条件。

正确答案

充分非必要

解析

解析已在路上飞奔，马上就到！

知识点

指数函数的图像变换

题型：填空题

分值: 4分

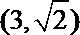
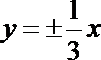
3．若双曲线经过点，且渐近线方程是，则这条双曲线的方程是_________．

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

导数的运算

题型：填空题

分值: 4分

4．若将一枚硬币连续抛掷三次，则出现“至少一次正面向上”的概率为_________．

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

二次函数的应用

题型：填空题

分值: 4分

5．下图是一个算法的程序框图，该算法所输出的结果是_________．

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

设计程序框图解决实际问题

题型：填空题

分值: 4分

6．已知正三棱锥主视图如图所示，其中中，，则这个正三棱锥的左视图的面积为_________

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

复合函数的单调性

题型：填空题

分值: 4分

8．如果一个球的外切圆锥的高是这个球半径的3倍，那么圆锥侧面积和球面积的比为_________．

正确答案

3：2

解析

解析已在路上飞奔，马上就到！

知识点

幂函数的概念、解析式、定义域、值域

题型：填空题

分值: 4分

13．对，设抛物线，过任作直线l与抛物线交与两点，则数列的前项和为_________．

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

对数函数的定义

题型：填空题

分值: 4分

11．已知函数的最小正周期为，将的图像向左平移个单位长度，所得图像关于y轴对称，则的值是_________ ．

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

复合函数的单调性

题型：填空题

分值: 4分

12．动点在不等式组表示的平面区域内部及其边界上运动，则的取值范围是_________．

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

幂函数的概念、解析式、定义域、值域

题型：填空题

分值: 4分

14．设数列是公差为的等差数列，是互不相等的正整数，若，则．请你用类比的思想，对等差数列的前项和为，写出类似的结论_________。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

复合函数的单调性

单选题本大题共4小题，每小题5分，共20分。在每小题给出的4个选项中，有且只有一项是符合题目要求。

题型：单选题

分值: 5分

15．在的展开式中，只有第5项的二项式系数最大，则展开式中常数项是（）

A-7

B-28

D28

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

复合函数的单调性

题型：单选题

分值: 5分

18．已知函数是定义域在上的奇函数，且时，，则关于在上零点的说法正确的是（）

A 有4个零点，其中只有一个零点在内

B 有4个零点，其中只有一个零点在内，两个在内

C 有5个零点都不在内

D 有5个零点，Z正零点中一个在内，一个在

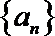
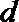
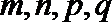
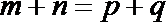
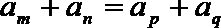
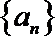
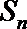
正确答案

解析

解析已在路上飞奔，马上就到！

知识点

幂函数的概念、解析式、定义域、值域

题型：单选题

分值: 5分

16．已知平面，，直线，若，，则（）

A垂直于平面的平面一定平行于平面

B垂直于直线的直线一定垂直于平面

C垂直于平面的平面一定平行于直线

D垂直于直线的平面一定与平面，都垂直

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

线面角和二面角的求法

题型：单选题

分值: 5分

17．已知抛物线上一点到其焦点的距离为，双曲线的左顶点为，若双曲线一条渐近线与直线平行，则实数等于（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

幂函数的概念、解析式、定义域、值域

简答题（综合题）本大题共74分。简答应写出文字说明、证明过程或演算步骤。

题型：简答题

分值: 13分

19．在锐角中，，，分别为内角，，所对的边，且满足．

（1）求角的大小；

（2）若，且，，求的值．

正确答案

（1）因为

所以

因为

所以

又为锐角，则

（2）由（1）可知，．因为

根据余弦定理，得

整理，得

由已知，则

又，可得，

于是

解析

解析已在路上飞奔，马上就到！

知识点

导数的加法与减法法则

题型：简答题

分值: 13分

20．如图四棱锥中，底面是平行四边形，，平面，，，是的中点．

（1）求证：平面；

（2）试在线段上确定一点，使∥平面，并求三棱锥-的体积．

正确答案

解：（1）证明：四边形是平行四边形，

，

平面

，又，

，

平面．

（2）设的中点为，

在平面内作于，

则平行且等于，连接，

则四边形为平行四边形，

∥，平面，平面，

∥平面，

为中点时，∥平面

设为的中点，连结，

则平行且等于，

平面，平面，

．

解析

解析已在路上飞奔，马上就到！

知识点

平行关系的综合应用

题型：简答题

分值: 14分

21．甲、乙两地相距1004千米，汽车从甲地匀速驶向乙地，速度不得超过120千米/ 小时，已知汽车每小时的运输成本（以1元为单位）由可变部分和固定部分组成：可变部分与速度（千米/ 小时）的平方成正比，比例系数为，固定部分为元．

（1）把全部运输成本元表示为速度（千米/小时）的函数，并指出这个函数的定义域；

（2）为了使全部运输成本最小，汽车应以多大速度行驶？

正确答案

（1）每小时运输成本为，

全程行驶时间为小时，

．

（2），

当且仅当，即时等号成立，

若，

当时，

若，

易证（略）函数在单调递减，

当时，．

解析

解析已在路上飞奔，马上就到！

知识点

函数单调性的性质

题型：简答题

分值: 16分

22．已知的顶点A、B在椭圆

（1）当AB边通过坐标原点O时，求AB的长及的面积；

（2）当，且斜边AC的长最大时，求AB所在直线的方程．

正确答案

（1）因为且AB通过原点（0，0），

所以AB所在直线的方程为

由得A、B两点坐标分别是

A（1，1），B（-1，-1）。

又的距离。

（2）设AB所在直线的方程为

由

因为A，B两点在椭圆上，

所以即

设A，B两点坐标分别为，则

且

又的距离，

边最长。（显然）

所以，AB所在直线的方程为

解析

解析已在路上飞奔，马上就到！

知识点

利用导数求参数的取值范围

题型：简答题

分值: 18分

23．设，等差数列中，，记=，令，数列的前n项和为．

（1）求的通项公式和；

（2）求证：；

（3）是否存在正整数，且，使得成等比数列？若存在，求出的值，若不存在，说明理由。

正确答案

（1）设数列的公差为

由，

解得，=3 ， ∴

∵

∴Sn==

（2）

∴

（3）由（2）知，

∴ ，

∵ 成等比数列

∴ 即

当时，7，=1，不合题意

当时，，=16，符合题意

当时，，无正整数解

当时，

则，而

所以，此时不存在正整数m，n，且1<m<n，使得成等比数列

综上，存在正整数m=2，n=16，且1<m<n，使得成等比数列

另解：（1）设数列的公差为

由

解得，=3

∴

∵

∴Sn==

（2）

∴

（3）由（2）知，

∴

∵成等比数列

∴

取倒数再化简得

当时，，=16，符合题意

而

所以，此时不存在正整数m、n ，且1<m<n，使得成等比数列

综上，存在正整数m=2，n=16，且1<m<n，使得成等比数列

解析

解析已在路上飞奔，马上就到！

知识点

幂函数的概念、解析式、定义域、值域

文科数学 热门试卷

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

文科数学热门试卷