- 真题试卷
- 模拟试卷
- 预测试卷
2.已知

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.若
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.函数
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.若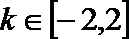
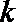
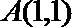
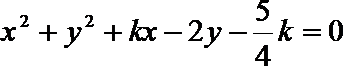
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.函数
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
1.已知集合


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.已知函数


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.已知点An(n,an)(n∈N*)都在函数y=

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.已知某几何体的三视图如图,其中正(主)视图中半圆的半径为1,则该几何体的体积为( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.下列命题中为真命题的是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12. 设




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.如图1所示,正△ABC中,CD是AB边上的高,E、F分别是AC、BC的中点.现将△ACD沿CD折起,使平面
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14.已知

正确答案
79
解析
解析已在路上飞奔,马上就到!
知识点
15.已知正数x、y,满足
正确答案
18
解析
解析已在路上飞奔,马上就到!
知识点
16.设


(1)
(2)

(3)
(4)
其中正确判断的序号( ).
正确答案
(1)(2)(4)
解析
解析已在路上飞奔,马上就到!
知识点
13.按如图所示的程序框图运行后,输出的结果是63,则判断框中的整数M的值是( ).
正确答案
5
解析
解析已在路上飞奔,马上就到!
知识点
18.某市为了了解今年高中毕业生的体能状况,从本市某校高中毕业班中抽取一个班进行铅球测试,成绩在8.0米(精确到0.1米)以上的为合格.把所得数据进行整理后,分成6组画出频率分布直方图的一部分(如图),已知从左到右前5个小组的频率分别为0.04,0.10,0.14,0.28,0.30 .第6小组的频数是7.
(1)求这次铅球测试成绩合格的人数;
(2)若由直方图来估计这组数据的中位数,指出它在第几组内,并说明理由;
(3)若参加此次测试的学生中,有9人的成绩为优秀,现在要从成绩优秀的学生中,随机选出2人参加“毕业运动会”,已知

正确答案
解:(1)第6小组的频率为1-(0.04+0.10+0.14+0.28+0.30)=0.14,
∴此次测试总人数为
∴第4、5、6组成绩均合格,人数为(0.28+0.30+0.14)×50=36(人).
(2)直方图中中位数两侧的面积相等,即频率相等.前三组的频率和为0.28,前四组的频率和为0.56,∴中位数位于第4组内.
(3)设成绩优秀的9人分别为

共36种,其中

∴

解析
解析已在路上飞奔,马上就到!
知识点
19.已知函数
(1)若曲线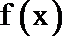
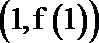
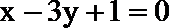
(2)当0<a<1时,求函数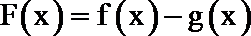
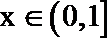
正确答案
略
解析
解析已在路上飞奔,马上就到!
知识点
21.已知数列




(1)求数列

(2)数列




正确答案
解:(1)设


由

因此
又
从而
(2)
令
两式相减得

解析
解析已在路上飞奔,马上就到!
知识点
17.设函数
(1)求
(2)若函数




正确答案
(1)

故
(2)解法一: 在

它关于
由题设条件,点

从而
当

因此

解法二:因区间

且

故



由(1)知
当
因此

解析
解析已在路上飞奔,马上就到!
知识点
22.已知函数

(1)求函数
(2)若直线


(3)设



正确答案
解:(1)

在区间




所以,



(2)设切点坐标为
则
解得

(3)
则
解

所以,在区间

在区间

当



所以

当



所以

当



综上所述,当


当



当


解析
解析已在路上飞奔,马上就到!
知识点
20.如图,已知在直四棱柱ABCD-A1B1C1D1中,
(1)求证:
(2)设E是DC上一点,试确定E的位置,使得D1E//平面A1BD,并说明理由。
正确答案
(1)设


则四边形






又


(2)证明:DC的中点即为E点,
连D1E,BE
∴四边形ABED是平行四边形,
∴AD


∴四边形A1D1EB是平行四边形

∵D1E
∴D1E//平面A1BD
解析
解析已在路上飞奔,马上就到!