- 真题试卷
- 模拟试卷
- 预测试卷
1.复数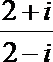
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.设




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.如果函数


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.设曲线



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.一个棱锥的三视图如右图所示,则它的体积为( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2.已知



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.设





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.若函数



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.函数
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.已知






正确答案
2
解析
解析已在路上飞奔,马上就到!
知识点
14.若存在


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15.选做题,从下面三题中任选一题作答。
(1).(选修4—4坐标系与参数方程)极坐标方程分别为

(2).(选修4—5 不等式选讲)如果关于x的不等式

(3).(选修4—1 几何证明选讲)如图,AD是⊙O的切线,AC是⊙O的弦,过C作AD的垂线,垂足为B,CB与⊙O相交于点E,AE平分
正确答案
(1)
(2)a>-1;
(3)
解析
解析已在路上飞奔,马上就到!
知识点
12.设变量



正确答案
4
解析
解析已在路上飞奔,马上就到!
知识点
13.若


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18.某日用品按行业质量标准分成五个等级,等级系数X依次为1.2.3.4.5.现从一批该日用品中随机抽取20件,对其等级系数进行统计分析,得到频率分布表如下:
(I)若所抽取的20件日用品中,等级系数为4的恰有3件,等级系数为5的恰有2件,求a、b、c的值;
(II)在(1)的条件下,将等级系数为4的3件日用品记为x1,x2,x3,等级系数为5的2件日用品记为y1,y2,现从x1,x2,x3,y1,y2,这5件日用品中任取两件(假定每件日用品被取出的可能性相同),写出所有可能的结果,并求这两件日用品的等级系数恰好相等的概率。
正确答案
解:(I)由频率分布表得
因为抽取的20件日用品中,等级系数为4的恰有3件,
所以
等级系数为5的恰有2件,所以
从而
所以
(II)从日用品
所有可能的结果为:

设事件A表示“从日用品

又基本事件的总数为10,
故所求的概率
解析
解析已在路上飞奔,马上就到!
知识点
20.已知

(1)若



(2)求

正确答案
(1)

又当


所以,曲线



(2)令


当





当





当





故


故当


当


综上所述,
解析
解析已在路上飞奔,马上就到!
知识点
21.已知抛物线













(1)若抛物线




(2)是否存在实数



正确答案
(1)




(或利用



(2)联立方程



则






得
若存在实数



即


即






解析
解析已在路上飞奔,马上就到!
知识点
17.已知

(1)求函数
(2)函数

正确答案
(1)由已知可得


所以函数

(2)把

得到函数
再把


得到函数
或:把

得到函数
再把

得到函数
解析
解析已在路上飞奔,马上就到!
知识点
19.如图,在四棱锥






(1)求四棱锥
(2)侧棱



正确答案
(1)

则有






(2)



证法一:设



















证法二:设











同理,由


又



又



解析
解析已在路上飞奔,马上就到!
知识点
16.已知数列

(1)令

(2)求
正确答案
(1)证
当
所以

(2)解由(1)知
当
当

所以
解析
解析已在路上飞奔,马上就到!






































































