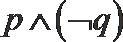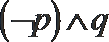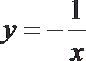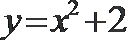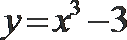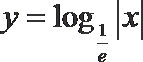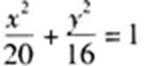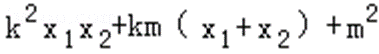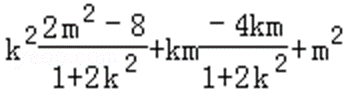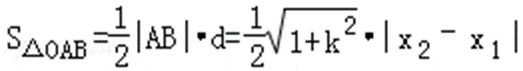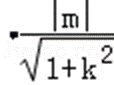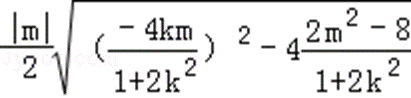- 真题试卷
- 模拟试卷
- 预测试卷
1.若

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2.已知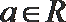
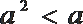
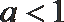
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.已知命题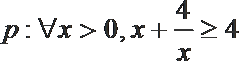

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.若变量


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.设函数

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.已知

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.下列函数中,与函数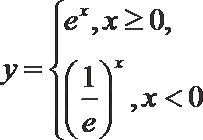
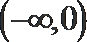
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.设函数




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.设函数



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.正项等比数列


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.已知向量
正确答案
1
解析
解析已在路上飞奔,马上就到!
知识点
13.计算:
正确答案
1
解析
解析已在路上飞奔,马上就到!
知识点
14.若椭圆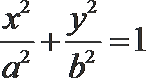
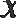
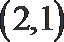
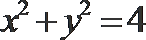
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15.棱长为4的正方体被一平面截成两个几何体,其中一个几何体的三视图如图所示,那么该几何体的体积是 ( ) .
正确答案
32
解析
解析已在路上飞奔,马上就到!
知识点
12.设

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.在

(I)求角C的大小;
(II)若


正确答案
(I)由2ccosA=2b﹣
利用正弦定理化简得:2sinCcosA=2sinB﹣
即2sinCcosA=2sin(A+C)﹣
整理得:
2sinCcosA=2sinAcosC+2cosAsinC﹣
即sinA(2cosC﹣
∵sinA≠0,
∴2cosC﹣

则C=
(Ⅱ)∵S△ABC=




∴a=4
由余弦定理得:
c2=a2+b2﹣2abcosC=48+4﹣2


解得:c=2
由正弦定理

sinA=


解析
解析已在路上飞奔,马上就到!
知识点
17.如图所示,在直三棱柱
(1)证明:
(2)证明:
正确答案
证明:(1)∵三棱柱ABC﹣A1B1C1为直三棱柱,
∴ AA1⊥平面ABC,
又CD⊂平面ABC,
∴ AA1⊥CD,
由于AA1∩AB=A,
∴ CD⊥平面AB1,
又AB1⊂平面AB1,CD⊥AB1,
AB1⊥A1C,CD∩A1C=C
所以:AB1⊥平面A1CD,
又A1D⊂平面A1CD,
∴ AB1⊥A1D.
(2)连接AC1交A1C于点F,
连接C1B和FD,
∵ 四边形A1ACC1是平行四边形,
F是AC1的中点,D是AB的中点,
∴ 在△AC1B中,FD∥BC1
又BC1⊄平面A1CD,
∴ BC1∥平面A1CD.
解析
解析已在路上飞奔,马上就到!
知识点
20.已知椭圆
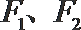
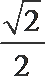

(I)求椭圆的方程;
(II)证明:
正确答案
(I)由椭圆的离心率为
可得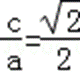

又2a=|AF1|+|AF2|=
∴a=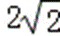
∴b2=4,
∴椭圆方程为: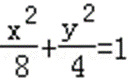
(Ⅱ)设直线AB的方程为y=kx+m,
再设A(x1,y1),B(x2,y2),
联立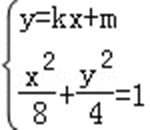
可得(1+2k2)x2+4kmx+2m2﹣8=0
△=(4km)2﹣4(1+2k2)(2m2﹣8)=8(8k2﹣m2+4)>0,

∵
∴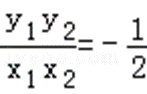
∴
又y1y2=(kx1+m)(kx2+m)
=
=
=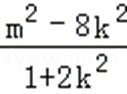
∴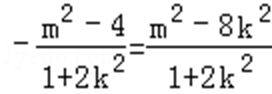
∴﹣(m2﹣4)=m2﹣8k2,即4k2+2=m2,
设原点到直线AB的距离为d,
则
=
=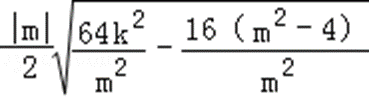
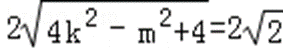
∴当直线斜率不存在时,有A(
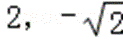
S△OAB=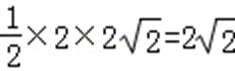
即△OAB的面积为定值2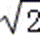
解析
解析已在路上飞奔,马上就到!
知识点
21.设函数
(I)当

(II)设A、B是曲线





正确答案
(I)函数的定义域为(0,+∞),
则f′(x)=
当m=

令f′(x)=0,则x=2或x=
当x变化时,f′(x),f(x)变化时,
∴当x=


当x=2时,f(x)的极大值为f(2)=
(Ⅱ)设A(x1,y1),B(x2,y2),(0<x1<x2),
由题意得f′(x1)=f′(x2)=0,
又f′(x)=
∴x1,x2是方程x2﹣2mx+1=0的两个正根,
故x1x2=1,判别式△=4m2﹣4>0,即m2>1,
f(x1)﹣f(x2)=mlnx1﹣

=m(lnx1﹣lnx2)﹣
=m(lnx1﹣lnx2)﹣(x1﹣x2),
若存在实数m,使得m﹣k=1,
则k=
∴
即
即lnx1﹣lnx2=x1﹣x2,
∵x1x2=1,0<x1<x2,
∴x1﹣
令h(t)=t﹣
h′(t)=1+

∴h(t)在(0,1)上单调递增,
∴h(t)<h(1)=1﹣1﹣2ln1=0,
即x1﹣
故不存在这样的m,使m﹣k=1.
解析
解析已在路上飞奔,马上就到!
知识点
18.等差数列

(I)求
(II)数列





正确答案
(Ⅰ)设等差数列{an}的公差是d,
∵S3=15,a5+a9=30,
∴
解得a1=3,d=2,
∴an=3+(n﹣1)×2=2n+1,
Sn=
证明:(Ⅱ)由(Ⅰ)得,
bn(Sn﹣n)=2,则bn(n2+n)=2,
∴


∴Tn=b1+b2+…+bn
=2[(1


=2(1﹣
∴对于任意正整数n,有Tn<2成立.
解析
解析已在路上飞奔,马上就到!
知识点
19.某公司生产的商品A每件售价为5元时,年销售10万件,
(1)据市场调查,若价格每提高一元,销量相应减少1万件,要使销售收入不低于原销售收入,该商品的销售价格最多提高多少元?
(2)为了扩大该商品的影响力,公司决定对该商品的生产进行技术革新,将技术革新后生产的商品售价提高到每件


正确答案
(1)设商品的销售价格提高a元,
则销售量减少10﹣a万件,
则(10﹣a)(5+a)≥50,
即a2﹣5a≤0,解得0≤a≤5,
故商品的销售价格最多提高5元.
(2)由题意知,改革后的销售收入为mx万元,
若使技术革新后的该商品销售收入等于原销售收入与总投入之和,
则只需要满足mx=

即m=






当且仅当

答:销售量m至少应达到
才可能使技术革新后的该商品销售收入等于原销售收入与总投入之和.
解析
解析已在路上飞奔,马上就到!