- 真题试卷
- 模拟试卷
- 预测试卷
13.已知









正确答案
3
解析
解析已在路上飞奔,马上就到!
知识点
6.10张奖券中只有3张有奖,5个人购买,每人一张,至少有1人中奖的概率是_______________
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.若正数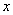
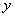
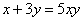
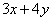
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.设点





正确答案
2
解析
解析已在路上飞奔,马上就到!
知识点
10.已知等差数列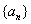
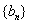
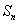
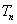
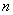

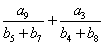
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12.已知正三棱锥





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14.集合







正确答案
2015
解析
解析已在路上飞奔,马上就到!
知识点
4.“


正确答案
充分不必要
解析
解析已在路上飞奔,马上就到!
知识点
3.直线

正确答案
-7
解析
解析已在路上飞奔,马上就到!
知识点
11.已知


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.将函数


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
1.已知复数:
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2.若

正确答案
3
解析
解析已在路上飞奔,马上就到!
知识点
9.已知



正确答案
15
解析
解析已在路上飞奔,马上就到!
知识点
15.函数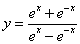
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18.如果数列


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.过抛物线
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17.将参加夏令营的600名学生编号为:001,002,……600,采用系统抽样方法抽取一个容量为50的样本,且随机抽得的号码为003.这600名学生分住在三个营区,从001到300在第Ⅰ营区,从301到495住在第Ⅱ营区,从496到600在第Ⅲ营区,三个营区被抽中的人数依次为 ( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19.已知向量




(1)求角
(2)若


正确答案
(1)








(2)由

及




解析
解析已在路上飞奔,马上就到!
知识点
20.如图,在长方体



(1)求异面直线

(2)当



正确答案
(1) 以









所以 其所成角为
解二:三垂线定理;
解三:实在不会做就硬做
(2) 

过



则


设点






解析
解析已在路上飞奔,马上就到!
知识点
21.如图,已知椭圆






(1)若圆


(2)当圆


(3)写出一个定圆的方程,使得无论点

正确答案
(1)解法一:因为圆









圆


解法二:设



所以


于是点


圆


(2)设圆




设




所以点



所以直线

(3)以原点为圆心,

探究过程为:设圆


因为
所以当原点为定圆圆心,半径

解析
解析已在路上飞奔,马上就到!
知识点
23.已知函数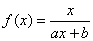


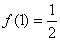
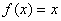
(1)求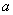
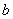
(2)在直角坐标系中,求定点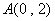
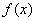
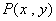
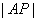
(3)当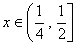

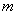
正确答案
(1)由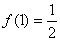

又
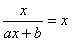

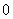
若无解,则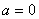

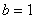
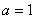
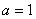

(若化为一元二次方程讨论,得出正确结论也可)
(2)由(1)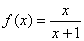

令


所以,当
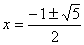
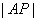
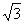
(3)因为


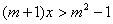
当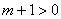

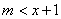

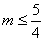
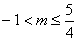
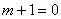
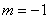
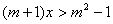
当
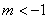
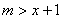
因为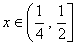
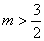

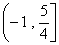
(3)的另一解法,把不等式看作关于
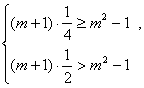
解析
解析已在路上飞奔,马上就到!
知识点
22.已知函数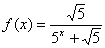

(1)求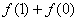
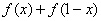
(2)若数列
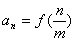


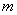
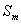
(3)设数列

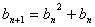



正确答案
(1)
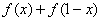

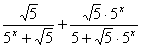
(2)由(1)得 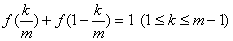
由
得
由①+②, 得
(3) ∵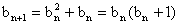
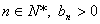
∴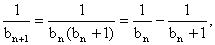

∴
∵
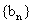
∴
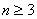
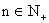

∵
∴
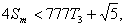
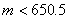

∴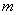
解析
解析已在路上飞奔,马上就到!