- 真题试卷
- 模拟试卷
- 预测试卷
4．已知f（x）＝
A
B
C
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
6．已知等差数列{
A1
B－1
C2
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
3．已知P（x0，y0）是直线L：Ax＋By＋C＝0外一点，则方程Ax＋By＋C＋（Ax0＋By0＋C）＝0（ ）
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
5．已知一个几何体的三视图如图所示，则该几何体的表面积为（ ）
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
8．已知命题p：
Ap∧q
Bp∨（
Cp∧（
D（
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
9．已知等比数列{
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
1．已知全集U＝R，集台M＝{x｜
AM∩N＝M
BM∪N＝N
CM∩（CUN）＝
D（C UM）∩N＝
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
2．设z＝1－i （i是虚数单位），则
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
7．执行下边的程序框图，若t∈[－1，2]，则S∈（ ）
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
10．已知函数f（x）＝sin（2x＋θ）＋
A
B
C
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
11．已知F1，F2分别是双曲线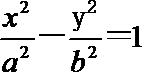
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
12．已知f（x）是定义在R上的偶函数，对任意x∈R，都有f（2＋x）＝－f（x），且当x∈[0，1]时，f（x）＝－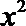
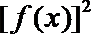
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
16．已知函数f（x）＝
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
15．边长是2
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
13．已知向量a＝（λ，1），b＝（λ＋2，1），若｜a＋b｜＝｜a－b｜，则实数λ＝______．
正确答案
-1
解析
解析已在路上飞奔，马上就到！
知识点
14．如图是甲、乙两名篮球运动员2013年赛季每场比赛得分的茎叶图，则甲、乙两人比赛得分的中位数之和为_____________．
正确答案
54
解析
解析已在路上飞奔，马上就到！
知识点
17． 在△ABC中，角A，B，C所对的边分别为a，b，c，且cosA＝
（Ⅰ）求
（Ⅱ）若a＝
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
18． 某企业员工500人参加“学雷锋”志愿活动，按年龄分组：第1组[25，30），第2组[30，35），第3组[35，40），第4组[40，45），第5组[45，50），得到的频率分布直方图如图所示．
（Ⅰ）上表是年龄的频率分布表，求正整数a，b的值；
（Ⅱ）现在要从年龄较小的第1，2，3组中用分层抽样的方法抽取6人，年龄在第1，2，3组的人数分别是多少?
（Ⅲ）在（Ⅱ）的前提下，从这6人中随机抽取2人参加社区宣传交流活动，求恰有1人年龄在第3组的概率．
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
19． 如图，已知在四棱锥P－ABCD中，底面ABCD是边长为4的正方形，△PAD是正三角形，平面PAD⊥平面ABCD，E，F，G分别是PD，PC，BC的中点．
（Ⅰ）求证：平面EFG⊥平面PAD；
（Ⅱ）若M是线段CD上一点，求三棱锥M－EFG的体积．
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
20． 已知椭圆
（Ⅰ）求椭圆的方程；
（Ⅱ）若M是圆
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
21． 已知函数f（x）＝2lnx－
（Ⅰ）当a＝2时，求f（x）的图象在x＝1处的切线方程；
（Ⅱ）若函数g（x）＝f（x）－ax＋m在[
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
请在第22~24题中任选一题做答。
22.选修4—1：几何证明选讲
如图，△ABC内接于⊙O，AB＝AC，直线MN切⊙O于点C，弦BD∥MN，AC与BD相交于点E．
（Ⅰ）求证：△ABE≌△ACD；
（Ⅱ）若AB＝6，BC＝4，求AE．
23．选修4—4：坐标系与参数方程
已知曲线C的极坐标方程为ρ＝
（Ⅰ）把曲线C的极坐标方程和直线l的参数方程化为直角坐标方程，并说明曲线C的形状；
（Ⅱ）若直线l经过点（1，0），求直线l被曲线C截得的线段AB的长．
24．选修4—5：不等式选讲
设函数f（x）＝｜2x－1｜＋｜ax－3｜，x∈R．
（Ⅰ）若a＝1时，解不等式f（x）≤5；
（Ⅱ）若a＝2时，g（x）＝
正确答案
22.
23.
24.
解析
解析已在路上飞奔，马上就到！