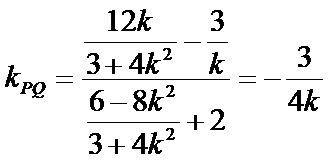- 真题试卷
- 模拟试卷
- 预测试卷
4.某三棱锥的侧视图和俯视图如图所示,
则该三棱锥的体积为 ( )
正确答案
解析
由三棱锥的侧视图和俯视图可知:侧棱PC垂直地面ABC,角ACB=90度,AC=6,BC=2,PB=4,据此可得:


考查方向
解题思路
由三棱锥的侧视图和俯视图可以知道此三棱锥大致图象如下图,根据立体图求相关的线段长。
易错点
立体感弱;计算能力差
知识点
6.在


正确答案
解析


考查方向
解题思路
根据所给条件,求出其他同角三角函数值
易错点
计算错误,忽略取值正负
知识点
8.将函数

正确答案
解析
将函数图像上各点的横坐标伸长到原来的3倍,可得到函数为:
再把函数图象向右平移


考查方向
解题思路
先得到变换后的函数,再根据函数图象对称性得到对称中心
易错点
变换规律掌握不好
知识点
9.双曲线

正确答案
解析
由题意可知,双曲线的一个渐近线方程为:



考查方向
解题思路
先求出渐近线方程,代入抛物线方程,从而推出a和c的关系。
易错点
计算能力差
知识点
1.已知集合

正确答案
解析



考查方向
解题思路
根据题意,先求出集合N,然后求出
易错点
集合N表示错误
知识点
3.在等比数列


正确答案
解析
因为等比数列中,




考查方向
解题思路
根据等比数列的性质求出公比q的值,然后求出前五项的积
易错点
计算错误;概念理解错误
知识点
5.若直线



正确答案
解析
因为两直线平行,所以

考查方向
解题思路
利用两条直线平行与斜率的关系即可得出
易错点
直线平行和直线垂直的斜率关系记忆混淆
知识点
7.若对任意非零实数


正确答案
解析
根据选择判断条件,可知
考查方向
解题思路
先知道新定义运算规则,进而判断输出结果
易错点
选择条件判断错误
知识点
2.复数
正确答案
解析
考查方向
解题思路
化成复数一般形式,根据一般形式判断虚数部分
易错点
忽略
知识点
10.在区间[0,2]上任取两个实数a,b,则函数
正确答案
解析
在区间[0,2]上任取两个数a,b,对应的平面区域为边长为2的正方形,面积为4,要想使函数在区间内没有零点,则函数的最小值应该大于0,即


考查方向
解题思路
结合二次函数的性质求出函数在区间内没有零点的等价条件,利用几何概型的概率公式即可得到结论
易错点
数型结合思想掌握不好,几何概型理解不透彻
知识点
12.已知函数


①当
②函数
③
④
其中正确命题个数是( )
正确答案
解析
因为f(x)为R上的奇函数,设x>0,-x<0,则



当


同理判断4正确,所以选B
考查方向
解题思路
根据函数的相关性质,结合子题目,依次判断
易错点
求导错误;
知识点
11.已知定义在R上的奇函数




正确答案
解析





考查方向
解题思路
先根据奇函数性质求出函数周期,进而求出f(-7)的值,然后判断实数a的取值范围
易错点
不能利用相关性质求出周期
知识点
13.已知a>0,b>0,且a+b=1,求
正确答案
4
解析

考查方向
解题思路
先变形,换成基本不等式的形式
易错点
不等式的性质应用时,等价转换错误
知识点
14.已知|






正确答案
解析
因为

考查方向
解题思路
先根据向量的数量积的定义,再根据向量垂直的性质求λ的值
易错点
平面向量及其应用
知识点
15.在



则
正确答案
解析
因为


所以

考查方向
解题思路
先根据余弦定理表示出
易错点
利用定理进行恒等变换时错误
知识点
16.已知三棱柱



正确答案
解析
因为侧棱垂直于底面,棱柱的体积为









考查方向
解题思路
利用垂直和棱柱体积求出AA1,再求出三角形ABC外接圆的半径,即可得到球的半径,从而求出球的表面积
易错点
计算能力;立体感
知识点
某市电视台为了宣传举办问答活动,随机对该市15~65岁的人群抽样了
19.分别求出
20.从第2,3,4组回答正确的人中用分层抽样的方法抽取6人,则第2,3,4组每组应各抽取多少人?
21.在20题的前提下,电视台决定在所抽取的6人中随机抽取2人颁发幸运奖,求:所抽取的人中第2组至少有1人获得幸运奖的概率.
正确答案
见解析
解析
第1组人数








考查方向
解题思路
图和表相互结合求得
易错点
计算错误;读取数据时有遗漏
正确答案
见解析
解析
第2,3,4组回答正确的人的比为


考查方向
解题思路
图和表相互结合求得
易错点
计算错误;读取数据时有遗漏
正确答案
见解析
解析
记抽取的6人中,第2组的记为

























故所求概率为
考查方向
解题思路
图和表相互结合求得
易错点
计算错误;读取数据时有遗漏
已知A、B分别是椭圆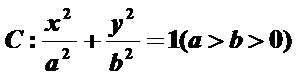

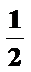

25.求椭圆C的方程;
26.已知点P是椭圆C上异于A、B的动点,直线l过点A且垂直于x轴,若过F作直线FQ垂直于AP,并交直线l于点Q,证明:Q、P、B三点共线.
正确答案
见解析
解析
抛物线的焦点F(1,0),∵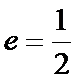
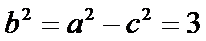
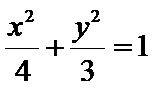
考查方向
解题思路
利用离心率和椭圆的性质以及抛物线的性质求椭圆的方程,利用直线与圆锥曲线方程证明三点共线。
易错点
计算能力弱
正确答案
见解析
解析
由25题知直线l的方程为x=-2,∵点P异于A,B,∴直线AP的斜率存在且不为0,设AP的方程为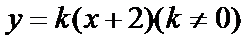
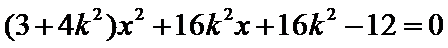
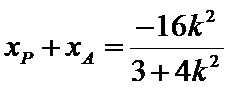
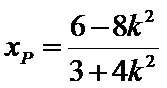
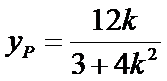
又∵QF⊥AP,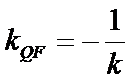
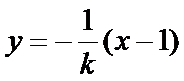
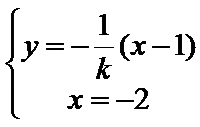
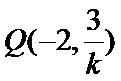
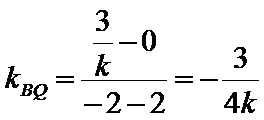
即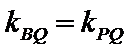
考查方向
解题思路
利用离心率和椭圆的性质以及抛物线的性质求椭圆的方程,利用直线与圆锥曲线方程证明三点共线。
易错点
计算能力弱
等差数列


17.求数列

18.设

正确答案
见解析
解析
设等差数列







考查方向
解题思路
第一问根据前N项和求通项公式,第二问用裂项相消的办法求数列的和
易错点
相关性质掌握不好;不会求数列的和
正确答案
见解析
解析
由(1)得
考查方向
解题思路
第一问根据前N项和求通项公式,第二问用裂项相消的办法求数列的和
易错点
相关性质掌握不好;不会求数列的和
已知平行四边形ABCD中,AB=4,E为 AB的中点,且△
22.F 是线段A1 C的中点,求证:BF //平面A1 DE ;
23.求证:A 1 D⊥CE ;
24.求点A1到平面BCDE的距离.
正确答案
见解析
解析
考查方向
解题思路
第一问根据特殊四边形的相关性质进行证明,第二问利用线面垂直证明线线垂直,第三问用和空间距离相关的性质求解。
易错点
辅助线作不出来;立体感不强
正确答案
见解析
解析
考查方向
解题思路
第一问根据特殊四边形的相关性质进行证明,第二问利用线面垂直证明线线垂直,第三问用和空间距离相关的性质求解。
易错点
辅助线作不出来;立体感不强
正确答案
见解析
解析
考查方向
解题思路
第一问根据特殊四边形的相关性质进行证明,第二问利用线面垂直证明线线垂直,第三问用和空间距离相关的性质求解。
易错点
辅助线作不出来;立体感不强
已知函数


27.求函数
28.当

29.若


正确答案
见解析
解析



考查方向
解题思路
先根据导数的性质求切线的斜率,进而求出参数的值,得到函数的解析式,利用导数的性质作出函数大致图像,结合图像,利用分类讨论思想求K的取值范围.
易错点
求导错误,函数性质理解错误;分类讨论有重有漏
正确答案
见解析
解析
令

当





∴
考查方向
解题思路
先根据导数的性质求切线的斜率,进而求出参数的值,得到函数的解析式,利用导数的性质作出函数大致图像,结合图像,利用分类讨论思想求K的取值范围.
易错点
求导错误,函数性质理解错误;分类讨论有重有漏
正确答案
见解析
解析




令













考查方向
解题思路
先根据导数的性质求切线的斜率,进而求出参数的值,得到函数的解析式,利用导数的性质作出函数大致图像,结合图像,利用分类讨论思想求K的取值范围.
易错点
求导错误,函数性质理解错误;分类讨论有重有漏
选修4—1;几何证明选讲.
如图,AB是⊙O的直径,C、F是⊙O上的两点,OC⊥AB,过点F作⊙O的切
30.求证:DE2=DB•DA;
31.若DB=2,DF=4,试求CE的长.
正确答案
见解析
解析
证明:连接OF.因为DF切⊙O于F,所以∠OFD=90°.所以∠OFC+∠CFD=90°.因为OC=OF,所以∠OCF=∠OFC.因为CO⊥AB于O,所以∠OCF+∠CEO=90°.
所以∠CFD=∠CEO=∠DEF,所以DF=DE.因为DF是⊙O的切线,所以DF2=DB•DA.
所以DE2=DB•DA.
考查方向
解题思路
利用辅助线,做出相似三角形,根据相似求出相关线段的长
易错点
辅助线,三角形相似条件找不准
正确答案
见解析
解析






考查方向
解题思路
利用辅助线,做出相似三角形,根据相似求出相关线段的长
易错点
辅助线,三角形相似条件找不准