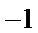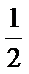- 真题试卷
- 模拟试卷
- 预测试卷
1．已知复数
A0
B
C2
D-2
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
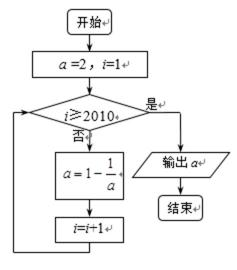
2．已知某程序框图如图所示，则执行该程序后输出的结果是（ ）
A
B1
C2
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
3．已知非零向量
A
B
C
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
4．已知三条不重合的直线m、n、l与两个不重合的平面α、β，有下列命题：
①若m∥n，n⊂α，则m∥α；
②若l⊥α，m⊥β且l∥m，则α∥β；
③若m⊂α，n⊂α，m∥β，n∥β，则α∥β；
④若α⊥β，α∩β＝m，n⊂β，n⊥m，则n⊥α．
其中正确的命题个数是（ ）
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
5．如图是一个几何体的三视图，则该几何体的体积为（ ）
A2
B
C
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
6．已知抛物线
A
B
C
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
7．已知不等式组
A
B
C
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
8．△PAB所在的平面α和四边形ABCD所在的平面β垂直，且AD⊥α，BC⊥α，AD=4，BC=8，AB=6，∠APD=∠CPB，则点P在平面α内的轨迹是（ ）
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
9．已知向量
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
10．双曲线
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
11．圆
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
12．某食品厂为了检查一条自动包装流水线的生产情况，随机抽取该流水线上的40件产品作为样本称出它们的重量（单位：克），重量的分组区间为（490，495]，（495，500]，…，（510，515]，由此得到样本的频率分布直方图，如右图所示．根据此频率分布直方图，可知重量超过500克的产品共有________件．
正确答案
26
解析
解析已在路上飞奔，马上就到！
知识点
13．从含有三件正品和一件次品的4件产品中不放回地任意取两件，则取出的两件中恰有一件次品的概率__________．
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
14．已知
（Ⅰ）若
（Ⅱ）若
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
17． 如图，在四棱锥
（Ⅰ）求证：
（Ⅱ）求证：
（Ⅲ）求四棱锥
正确答案
（Ⅰ）证明：设
在
又
（Ⅱ）证明：
又
（Ⅲ）答案：
在
在
解析
解析已在路上飞奔，马上就到！
知识点
18． 设
（Ⅰ）若函数
（Ⅱ）当
正确答案
（Ⅰ）
（Ⅱ）答案略。
解析
解析已在路上飞奔，马上就到！
知识点
19． 设椭圆
（Ⅰ）若过
（Ⅱ）在（Ⅰ）的条件下，过右焦点
正确答案
（Ⅰ）由题意
又
所以
所以
又过
故所求椭圆方程为
（Ⅱ）由（）知
椭圆联立方程得
设交点为
则
若存在点
由于菱形对角线垂直，所以
又
由已知条件知
解析
解析已在路上飞奔，马上就到！
知识点
16．已知某单位有50名职工，从中按系统抽样抽取10名职工，分别统计这10名职工的体重（单位：公斤），获得体重数据的茎叶图如图所示.
（Ⅰ）求该样本的中位数、平均体重和方差；
（Ⅱ）从这10名职工中随机抽取两名体重不轻于73公斤的职工，求体重为76公斤的职工被抽取到的概率。
正确答案
（Ⅰ）中位数为：
平均体重为：
样本方差为：
（Ⅱ）设事件
从
基本事件为：
共有
事件
故所求概率为
解析
解析已在路上飞奔，马上就到！
知识点
15． 已知函数
（Ⅰ）求
（Ⅱ）在
正确答案
（Ⅰ）
由
所以函数
函数
（Ⅱ）由
又
解析
解析已在路上飞奔，马上就到！
知识点
20．对于数集
（Ⅰ）若
（Ⅱ）若X具有性质P，求证：1X，且当
（Ⅲ）若X具有性质P，且
正确答案
（Ⅰ）选取
所以x=2b，从而x=4.
（Ⅱ）证明：取
由
因为-1是X中唯一的负数，所以
故1
假设
选取
则
若
若
所以x1=1.
（Ⅲ）[答案法一]猜测
记
先证明：若
任取
当
因为
从而
假设
现用数学归纳法证明：
当n=2时，结论显然成立；
假设n=k时，
当n=k+1时，若
也有性质P，所以
取
若
所以
综上所述，
[答案法二]设
记
原点对称.
注意到-1是X中的唯一负数，
所以
由于
……
注意到
解析
解析已在路上飞奔，马上就到！