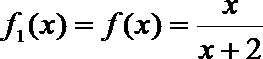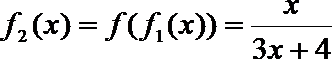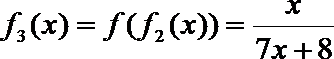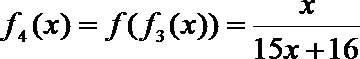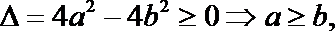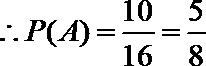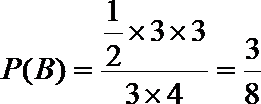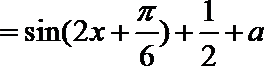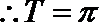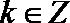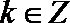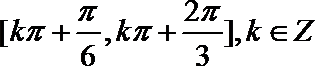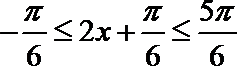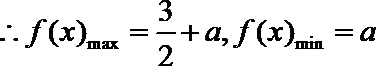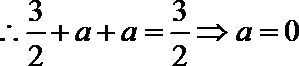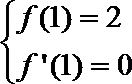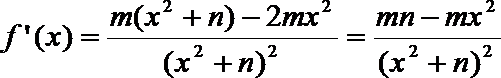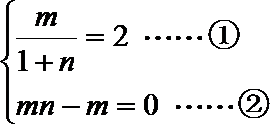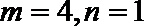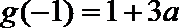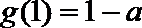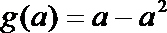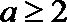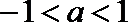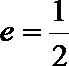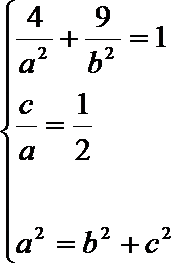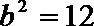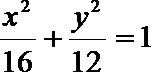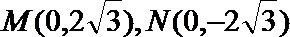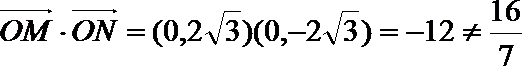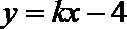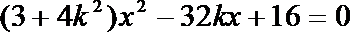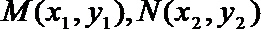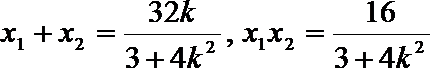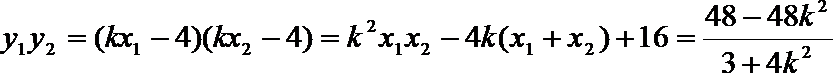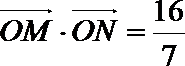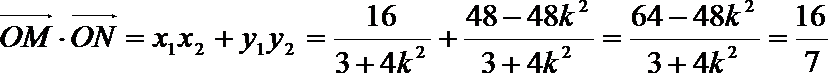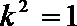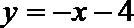- 真题试卷
- 模拟试卷
- 预测试卷
1.已知i为虚数单位,复数
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.“

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.执行右边的程序框图,输出S的值为( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.将函数

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2.设集合


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.已知向量


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.若



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.已知

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.已知某几何体的三视图如图所示,若该几何体的体积为24,则该几何体的底面积是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.已知抛物线


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7. 函数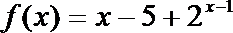
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12.若对任意的




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.设函数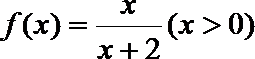
……
依此类推,归纳推理可得当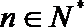
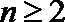
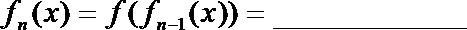
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
13.一组数据为15,17,14,10,15,17,17,14,16,12,设其平均数为m,中位数为n,众数为p,
则m,n,p的大小关系是_____________.
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15.若双曲线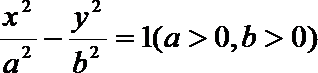

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14.已知变量


正确答案
2
解析
解析已在路上飞奔,马上就到!
知识点
18.设关于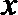
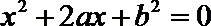
(1)若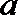
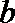
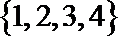
(2)若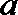
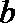
正确答案
(1)设事件A=“方程有实根”,记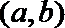
(1,1),(1,2),(1,3),(1,4),(2,1),(2,2),(2,3),(2,4)
(3,1),(3,2),(3,3),(3,4),(4,1),(4,2),(4,3),(4,4)
一共16种且每种情况被取到的可能性相同
∵关于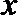
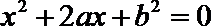
∴
∴事件A包含的基本事件有:
(1,1),(2,1),(2,2),(3,1),(3,2),(3,3),(4,1),(4,2),(4,3),(4,4)共10种
∴方程有实根的概率是
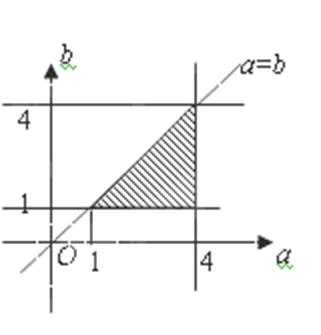
(2)设事件B=“方程有实根”,记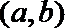
∵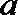
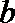
∴点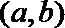
又满足: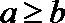
∴
∴方程有实根的概率是
解析
解析已在路上飞奔,马上就到!
知识点
20.如图所示,在四棱锥


(1)求证:
(2)求证:平面PDC
(3)求四棱锥
正确答案
(1)
连接EF,AC
∵四棱锥
∴对角线AC经过F点
又在
∴EF为
∴
又
∴
(2)∵底面ABCD是边长为a的正方形
∴
又侧面


∴
又
∴平面PDC
(3)过点P作AD的垂线PG,垂足为点G
∵侧面


∴

又
∴
∴
解析
解析已在路上飞奔,马上就到!
知识点
17.已知数列

(1)求数列
(2)若数列




正确答案
(1)
又当

∴
(2)由(1)可知

又
∴
又数列
∴
又
∴
∴
∴数列
解析
解析已在路上飞奔,马上就到!
知识点
19.设函数
(1)写出函数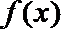
(2)当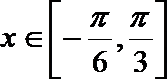
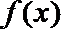

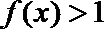
正确答案
(1)
令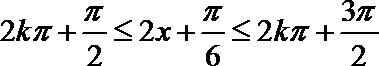
∴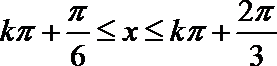
∴函数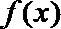
(2)由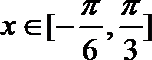
∴
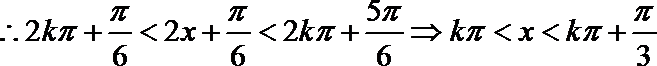
又
∴不等式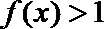
解析
解析已在路上飞奔,马上就到!
知识点
22.已知函数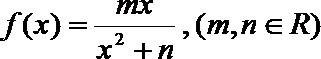
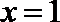
(1)求函数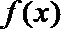
(2)求函数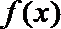
(3)设函数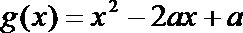
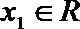
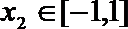
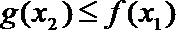

正确答案
(1)∵函数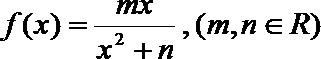
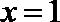
∴
又
∴
由②式得m=0或n=1,但m=0显然不合题意
∴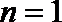
∴
经检验,当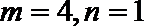
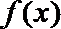
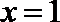
∴函数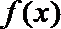
(2)∵函数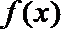
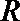
令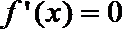
∴当x变化时,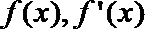
∴当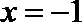
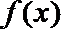
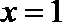
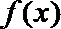
(3)依题意只需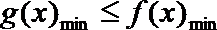
∵函数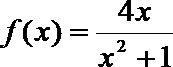
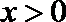
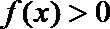
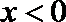
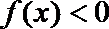
∴ 由(2)知函数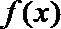
∴当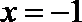
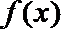
又对任意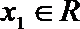
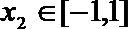
∴当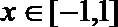
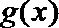
又
①当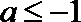
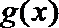
∴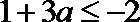
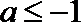
②当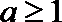
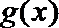
∴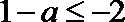
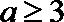
③当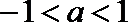
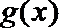
∴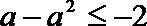
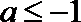
又∵
∴此时a不存在
综上所述,a的取值范围是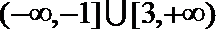
解析
解析已在路上飞奔,马上就到!
知识点
21.已知椭圆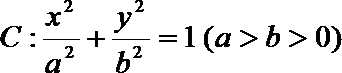
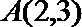
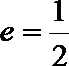
(1)求椭圆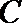
(2)是否存在过点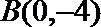
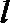
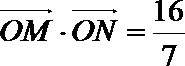
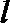
正确答案
(1)∵椭圆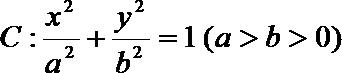
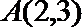
∴
解得: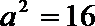
∴椭圆的方程为:
(2)假设存在过点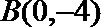
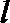
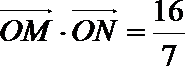
若直线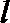
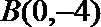
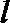
∴直线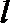
∴
∴
∴直线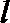
∴可设直线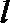
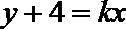
联立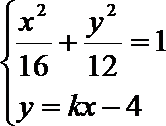
∵直线与椭圆相交于不同的两点M、N
∴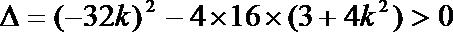
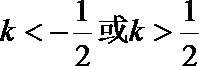
设
∴
∴
又
∴
化简得
∴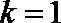
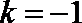
∴直线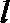
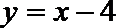
∴存在直线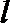
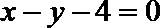
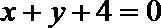
解析
解析已在路上飞奔,马上就到!