- 真题试卷
- 模拟试卷
- 预测试卷
1.已知命题p:

正确答案

解析
解析已在路上飞奔,马上就到!
知识点
2.设集合A={x|-1≤x≤2},B={x|0≤x≤4},则A∪B=( )
正确答案
[-1,4]
解析
解析已在路上飞奔,马上就到!
知识点
4.一个正四面体的四个面分别涂有红、黄、蓝、白四种颜色,若随机投掷该四面体两次,则两次底面颜色相同的概率是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.在




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.已知双曲线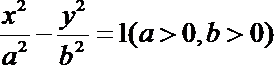
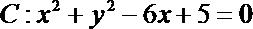
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.已知圆(x-2)2+y2=1经过椭圆
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.将函数y=sin(x+

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.已知正四棱柱的底面边长为2,高为3,则该正四棱柱的外接球的表面积为( )
正确答案
17π
解析
解析已在路上飞奔,马上就到!
知识点
3.设复数z1=1-2i,z2=x+i(x∈R),若z1·z2为实数,则x=( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.已知数列{an}的前n项和Sn=2n+n-1,则a1+a3=( )
正确答案
7
解析
解析已在路上飞奔,马上就到!
知识点
11.如图,平面四边形ABCD


正确答案
1
解析
解析已在路上飞奔,马上就到!
知识点
14.已知f(x)=x3,g(x)=-x2+x-

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12.若不等式4x-2x+1-a≥0在x∈[-1,1]上恒成立,则实数a的取值范围为( )
正确答案
(-∞,-1]
解析
解析已在路上飞奔,马上就到!
知识点
13.若f(n)为n2+1(n∈N*)的各位数字之和,如142+1=197,1+9+7=17,则f(14)=17.记f1(n)=f(n),f2(n)=f(f1(n)),…,fk+1(n)=f(fk(n)),k∈N*,则f2011(8)=( )
正确答案
11
解析
解析已在路上飞奔,马上就到!
知识点
15.已知△ABC的三个内角A、B、C所对的边分别为a、b、c,向量m=(sinA,1),n=(1,-
(1)求角A;
(2)若b+c=

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19.记公差d≠0的等差数列{an}的前n项和为Sn,已知a1=2+

(1)求数列{an}的通项公式an及前n项和Sn;
(2)记bn=an-



(3)试问:在数列{an}中是否存在三项ar,as,at(r<s<t,r,s,t∈N*)恰好成等比数列?若存在,求出此三项;若不存在,请说明理由。
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
20.已知函数f(x)=ax+x2-xlna(a>0,a≠1)。
(1)当a>1时,求证:函数f(x)在(0,+∞)上单调递增;
(2)若函数y=|f(x)-t|-1有三个零点,求t的值;
(3)若存在x1,x2∈[-1,1],使得|f(x1)-f(x2)|≥e-1,试求a的取值范围。
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17.某工厂去年新开发的某产品的年产量为100万只,每只产品的销售价为10元,固定成本为8元。今年,工厂第一次投入100万元的科技成本,并计划以后每年比上一年多投入100万元,预计产量每年递增10万只,投入n次后,每只产品的固定成本为g(n)=
(1)求k的值,并求出f(n)的表达式;
(2)问从今年起,第几年纯利润最高?最高纯利润为多少万元?
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18.如图,椭圆的中心为原点O,已知右准线l的方程为x=4,右焦点F到它的距离为2。
(1)求椭圆的标准方程;
(2)设圆C经过点F,且被直线l截得的弦长为4,求使OC长最小时圆C的方程。
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.如图,在四棱锥O—ABCD中,AD//BC,AB=AD=2BC,OB=OD,M是OD的中点。
(1)求证:MC//平面OAB;
(2)求证:BD⊥OA。
正确答案
解析
解析已在路上飞奔,马上就到!