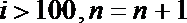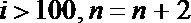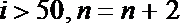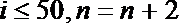- 真题试卷
- 模拟试卷
- 预测试卷
4.已知



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.将函数y=sin(2x+

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.如图所示的茎叶图表示甲、乙两人在5次综合测评中的成绩,其中一个数字被污损,则甲的平均成绩超过乙的平均成绩的概率为( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.已知函数
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2.

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3. 在


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.若



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
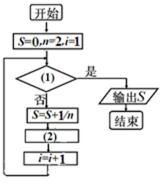
8.如图给出的是计算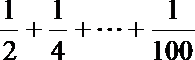
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6. 等比数列


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
1.已知全集U=R,集合A={x|
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11. 已知


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12. 已知某几何体的三视图如图所示,若该几何体的体积为24,则正视图中
正确答案
6
解析
解析已在路上飞奔,马上就到!
知识点
14.在△ABC中,D为边BC上一点,BD=



正确答案
60°
解析
解析已在路上飞奔,马上就到!
知识点
15.点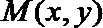
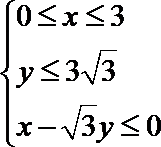
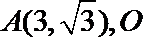
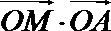
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
13.原对大于或等于


根据上述分解规律,

正确答案
31+33+35+37+39+41
解析
解析已在路上飞奔,马上就到!
知识点
18.在棱长为



(1)求证:

(2)求证:

(3)求三棱锥
正确答案
解: (1)证明:根据正方体的性质
因为

所以



(2)证明:
连接

所以
由于


因为



所以
(3)
解析
解析已在路上飞奔,马上就到!
知识点
19.已知数列


(1)证明:数列

(2)设

正确答案
解:(1)
(2)
解析
解析已在路上飞奔,马上就到!
知识点
16.已知


(1)求角C的大小;
(2)若
正确答案
(1)C= 
(2)a=2,b=4或a=4,b=2
解析
解析已在路上飞奔,马上就到!
知识点
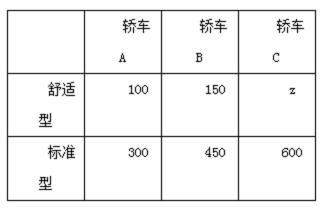
17.一汽车厂生产A,B,C三类轿车,每类轿车均有舒适型和标准型两种型号,某月的产量如右表(单(辆)位: 按类型分层抽样的方法在这个月生产的轿车中抽取50辆, 其中有A类轿车10辆
(1)求z的值;
(2)用分层抽样的方法在C类轿车中抽取一个容量为5的样本.将该样本看成一个总体,从中任取2辆,求至少有1辆舒适型轿车的概率;
(3)用随机抽样的方法从B类舒适型轿车中抽取8辆,经检测它们的得分如下:9.4, 8.6, 9.2, 9.6, 8.7, 9.3, 9.0, 8.2.把这8辆轿车的得分看作一个总体,从中任取一个数,求该数与样本平均数之差的绝对值不超过0.5的概率。
正确答案
解: (1)设该厂本月生产轿车为n辆,由题意得,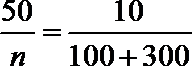
所以n=2000. z=2000-100-300-150-450-600=400
(2)设所抽样本中有m辆舒适型轿车,
因为用分层抽样的方法在C类轿车中抽取一个容量为5的样本,
所以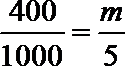
则从中任取2辆的所有基本事件为
(S1, B1), (S1, B2) , (S1, B3) (S2 ,B1), (S2 ,B2),
(S2 ,B3),( (S1, S2),(B1 ,B2), (B2 ,B3) ,(B1 ,B3)共10个,
其中至少有1辆舒适型轿车的基本事件有7个基本事件:
(S1, B1), (S1, B2) , (S1, B3) (S2 ,B1), (S2 ,B2), (S2 ,B3),( (S1, S2),
所以从中任取2辆,至少有1辆舒适型轿车的概率为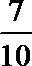
(3)样本的平均数为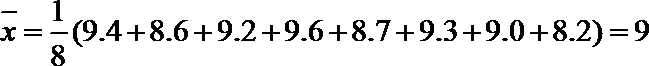
那么与样本平均数之差的绝对值不超过0.5的数为
9.4, 8.6, 9.2, 8.7, 9.3, 9.0这6个数,总的个数为8,
所以该数与样本平均数之差的绝对值不超过0.5的概率为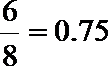
解析
解析已在路上飞奔,马上就到!
知识点
20.如图,


(1)求点M的轨迹C的方程;
(2)过点

正确答案
解:(1)设点



则



因为


将①代入②,得点

(2)由题意知,
当


此时


当

由
得
设A、B两点的坐标分别为

又由l与圆

所以
因为

所以|AB|的最大值为2
依题意,圆心

所以

当且仅当

解析
解析已在路上飞奔,马上就到!
知识点
21.设


(1)若

(2)若

(3)函数




正确答案
解:
(1)

由
(2)∵



∴

∵


而


由
令


∴




∴
(3)∵x1、x2是方程



解析
解析已在路上飞奔,马上就到!