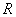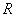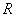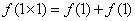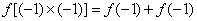- 真题试卷
- 模拟试卷
- 预测试卷
6.已知函数
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2.复数
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.如果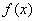
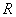
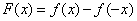
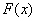
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.等比数列



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.若向量

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.设



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.曲线

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
1.集合


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.函数



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.函数
正确答案

解析
解析已在路上飞奔,马上就到!
知识点
9.设点






正确答案
2
解析
解析已在路上飞奔,马上就到!
知识点
12.三个数成等差数列,其比为3:4:5,又最小数加上1后,三个数成等比数列,那么原三个数是___________。
正确答案
15、20、25
解析
解析已在路上飞奔,马上就到!
知识点
13.若二次函数



正确答案

解析
解析已在路上飞奔,马上就到!
知识点
14.若




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15.已知:函数




(1)求:
(2)当

正确答案
解:(1)由最低点为

由





由点


∵

∴
(2)∵

当



当


故

解析
解析已在路上飞奔,马上就到!
知识点
16.已知:若





(1)求:数列


(2)若

正确答案
解:(1)设等差数列
(2)
解析
解析已在路上飞奔,马上就到!
知识点
20. 已知:函数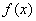
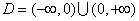
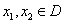
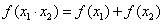
(1)求: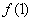
(2)判断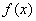
(3)如果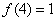
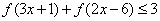
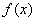
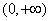
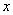
正确答案
(1)解:令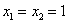
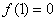
(2)证明:令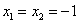
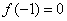
令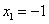
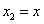

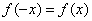
∴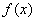
(3)∵
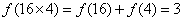
∴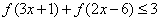
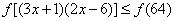
∵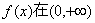
∴(1)等价于不等式组: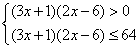
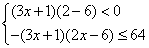
则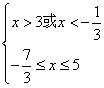

解析
解析已在路上飞奔,马上就到!
知识点
19.已知:对于数列


(1)若数列



(2)若数列

①设


②求:数列


正确答案
解:(1)依题意
(2)①由
∵


故



∵
∴

⑴-⑵得 
∴
解析
解析已在路上飞奔,马上就到!
知识点
17.已知:定义在R上的函数
(1)若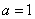
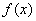
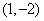
(2)若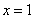
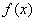
(3)若函数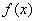

正确答案
解:(1)当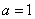
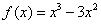
则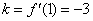
∴切线方程: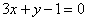
(2)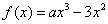
∵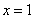
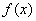
∴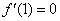
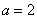
(3)①当a=0时,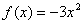
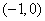
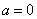
②当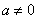
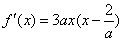
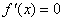
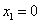
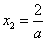
当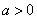
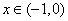
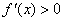
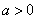
当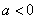
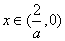

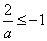

综上所述,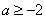
解析
解析已在路上飞奔,马上就到!
知识点
18.已知:向量


(1)若

(2)求:
正确答案
解:(1)
∵
(2)



∴当



解析
解析已在路上飞奔,马上就到!