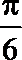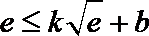- 真题试卷
- 模拟试卷
- 预测试卷
1.已知集合


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2.已知复数z满足
正确答案
解析
解析已在路上飞奔,马上就到!
知识点


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7. 设

①
②
③
④
其中正确命题的个数有( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.设



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3. 设


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.“m=
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.已知|





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8. 已知点P为


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.要得到函数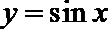
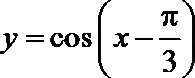
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.已知双曲线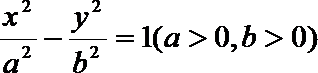
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12.设








正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15.过椭圆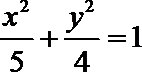
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.给出下列四个命题:
①设



②任意的锐角三角形

③平面上n个圆最多将平面分成
④空间中直角在一个平面上的正投影可以是钝角。
其中真命题的序号是( )(要求写出所有真命题的序号)。
正确答案
②④
解析
解析已在路上飞奔,马上就到!
知识点
13.已知对于任意实数



则这2009个实数解之和为 。
正确答案
0
解析
解析已在路上飞奔,马上就到!
知识点
14. 已知等差数



正确答案
n=12或13
解析
解析已在路上飞奔,马上就到!
知识点
19.已知正项数列



(1)求数列
(2)若



正确答案
(1)由题意知

当
当


整理得
所以数列
(2)

两式相减得
所以
所以
解析
解析已在路上飞奔,马上就到!
知识点
20.如图1,在直角梯形




(Ⅰ)若E为AD的中点,试在线段CD上找一点F,使EF∥平面ABC,并加以证明;
(Ⅱ)求证: BC⊥平面ACD;
(Ⅲ)求几何体A-BCD的体积。
正确答案
(Ⅰ)在CD上中点F, 使EF∥平面ABC(略)
(Ⅱ)在图1中,可得


取











∵

又
∴
另解:在图1中,可得

∵面







(Ⅲ)由(Ⅰ)可知


所以

解析
解析已在路上飞奔,马上就到!
知识点
17. 在








(Ⅰ)求角
(Ⅱ)设

正确答案
(Ⅰ)


∴

(Ⅱ)由
知
∴

由正弦定理得:
解析
解析已在路上飞奔,马上就到!
知识点
18. 为了在如图所示的直河道旁建造一个面积为5000m2的矩形堆物场,需砌三面砖墙BC、CD、DE,出于安全原因,沿着河道两边需向外各砌10m长的防护砖墙AB、EF,若当BC的长为

(1)y关于x的函数解析式y=f(x);
(2)若BC的长不得超过40m,则当BC为何值时,y有最小值,并求出这个最小值。
正确答案
解:(1)
(2)令
因为

所以
故当x=40m时,y取理最小值225m
解析
解析已在路上飞奔,马上就到!
知识点
21. 已知圆







(Ⅰ)求椭圆
(Ⅱ) 当点P在圆

正确答案
解:(Ⅰ)因为
所以椭圆C的标准方程为
(Ⅱ)当点P在圆O上运动时,
设


所以

所以直线O


所以
所以
当



解析
解析已在路上飞奔,马上就到!
知识点
22.若存在实常数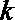
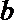
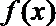
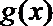
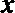
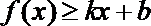
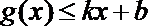
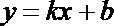
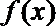
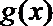
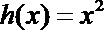
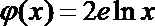
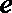
(1)求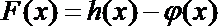
(2) 函数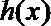
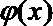
正确答案
(1) 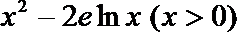
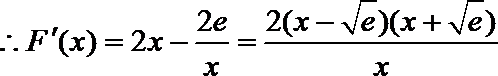

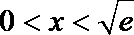
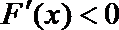
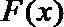
当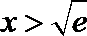
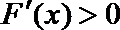
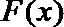
∴当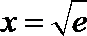
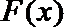
(2) 由(1)可知当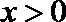
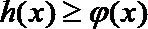

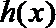
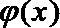
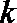

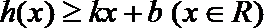
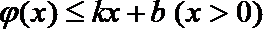
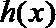
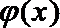

令
解析
解析已在路上飞奔,马上就到!