- 真题试卷
- 模拟试卷
- 预测试卷
7.某产品在某零售摊位的零售价x(单位:元)与每天的销售量y(单位:个)的统计资料如下表所示:由上表可得回归直线方程

正确答案
解析
由题意知

知识点
2.已知全集



正确答案
解析
由题意得:





知识点
3.已知函数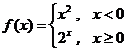
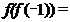
正确答案
解析
略。
知识点
10.已知函数
正确答案
解析
函数y=f(x)是一个非奇非偶函数,图象不关于原点对称,故排除选项A、C,又当x>0时,函数值大于0恒成立,故排除D,故选 B。
知识点
8.执行图1所示的程序框图,输出的a的值为()
正确答案
解析
根据程序框图,模拟运行如下:
输入S=1,a=3,
S=1×3=3,此时不符合S≥100,a=3+2=5,执行循环体,
S=3×5=15,此时不符合S≥100,a=5+2=7,故执行循环体,
S=15×7=105,此时符合S≥100,故结束运行,
∴输出n=7.故选:C。
知识点
1.复数
正确答案
解析
由

知识点
5.已知△




正确答案
解析
由正弦定理得:






知识点
6.下列关于命题的说法错误的是 ( )
正确答案
解析
因为命题“若x2-3x+2=0,则x=1”的逆否命题为“若x≠1,则x2-3x+2≠0”,所以A正确;由a=2能得到函数f(x)=logax在区间(0,+∞)上为增函数,反之,函数f(x)=logax在区间(0,+∞)上为增函数,a不一定大于2,所以“a=2”是“函数f(x)=logax在区间(0,+∞)上为增函数”的充分不必要条件,所以选项B正确;命题P:


知识点
9.已知F1,F2是双曲线
正确答案
解析
依题意可知双曲线的焦点为F1(﹣c,0),F2(c,0)
∴F1F2=2c∴三角形高是



代入双曲线方程得:
所以c4﹣a2c2﹣3a2c2=4a2c2﹣4a4整理得e4﹣8e2+4=0求得e2=4±2
∴e=
知识点
4.在平面直角坐标系中,从下列五个点:A(0,0),B(2,0),C(1,1),D(0,2),(2,2)中任取三个,这三点能构成三角形的概率是( )
正确答案
解析
从5个点中取3个点,列举得ABC,ABD,ABE,ACD,ACE,ADE,BCD,BCE,BDE,CDE共有10个基本事件,而其中ACE, BCD两种情况三点共线,其余8个均符合题意,故能构成三角形的概率为
知识点
11.曲线


正确答案
2
解析


知识点
12.设E,F分别是Rt△ABC的斜边BC上的两个三等分点,已知AB=3,AC=6,则
正确答案
10
解析
由已知中E,F分别是Rt△ABC的斜边BC上的两个三等分点,已知AB=3,AC=6,我们可以以A为坐标原点,AB、AC方向为X,Y轴正方向建立坐标系,分别求出向量

以A为坐标原点,AB、AC方向为X,Y轴正方向建立坐标系
∵AB=3,AC=6,
则A(0,0),B(3,0),C(0,6)
又∵E,F分别是Rt△ABC的斜边BC上的两个三等分点,则E(2,2),F(1,4)
则


知识点
15.若不等式

正确答案
解析
由于





知识点
13.已知数列{an}满足an=,则数列的前n项和为________。
正确答案
解析
所求的前n项和为,
知识点
14.已知椭圆C: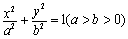
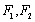
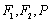
正确答案
解析
因为点P的横坐标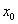
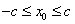
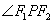
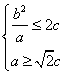
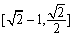
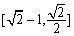
知识点
20.已知抛物线C:y2=2px(p>0)过点A(1,﹣2)。
(Ⅰ)求抛物线C的方程,并求其准线方程;
(Ⅱ)是否存在平行于OA(O为坐标原点)的直线L,使得直线L与抛物线C有公共点,且直线OA与L的距离等于
正确答案
见解析。
解析
(I)将(1,﹣2)代入抛物线方程求得p,则抛物线方程可得,进而根据抛物线的性质求得其准线方程。
(II)先假设存在符合题意的直线,设出其方程,与抛物线方程联立,根据直线与抛物线方程有公共点,求得t的范围,利用直线AO与L的距离,求得t,则直线l的方程可得。
(I)将(1,﹣2)代入抛物线方程y2=2px,
得4=2p,p=2
∴抛物线C的方程为:y2=4x,其准线方程为x=﹣1
(II)假设存在符合题意的直线l,其方程为y=﹣2x+t,
由
∵直线l与抛物线有公共点,
∴△=4+8t≥0,解得t≥﹣
又∵直线OA与L的距离d=

∵t≥﹣
∴t=1
∴符合题意的直线l存在,方程为2x+y﹣1=0
知识点
16.已知函数

(1)求
(2)若


正确答案
(1)
(2)
解析
(1)∵
(2)由


∵

∴
知识点
17.已知数列






(1)求

(2)若




正确答案
见解析。
解析
(1)∵



∴
∴

在



当




∴
∴

∴

知识点
19.如图所示,矩形













(Ⅰ)求证:

(Ⅱ)若

(Ⅲ)求四面体
正确答案
见解析。
解析
(Ⅰ)证明:因为四边形





所以 四边形
所以 

因为 



(Ⅱ)证明:连接

因为平面



所以 
又 


所以 


(Ⅲ)解:设




所以四面体

所以 
当且仅当


知识点
18.(本小题满分12分)已知函数
(Ⅰ)求
(Ⅱ)若




正确答案
见解析。
解析
(Ⅰ)∵

要使

从而△=

(Ⅱ)∵

∴

∴

∴



∵

∴

∴



知识点
21.对某校高三年级学生参加社区服务次数进行统计,随机抽取

根据此数据作出了频数与频率的统计表和频率分布直方图如下:
(Ⅰ)求出表中

(Ⅱ)若该校高三学生有240人,试估计该校高三学生参加社区服务的次数在区间
(Ⅲ)在所取样本中,从参加社区服务的次数不少于20次的学生中任选2人,求至多一人参加社区服务次数在区间
正确答案
见解析。
解析
(Ⅰ)由分组

因为频数之和为


因为

(Ⅱ)因为该校高三学生有240人,分组

所以估计该校高三学生参加社区服务的次数在此区间内的人数为
(Ⅲ)这个样本参加社区服务的次数不少于20次的学生共有