- 真题试卷
- 模拟试卷
- 预测试卷
1．设集合
A{（1，1），（-1，1）}
B{1}
C[0，2]
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
2．设
A
B
C
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
3．某几何体的三视图如图所示，则其表面积为（ ）
A8
B2
C
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
7．等比数列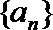
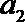
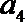
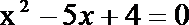
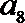
A16
B
C64
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
9.若向量
A
B—
C
D—
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
10．点P是双曲线
A
B
C
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
5．设
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
6．阅读下面的程序框图，运行相应的程序，则输出i的值为（ ）
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
8．曲线
A
B
C
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
4．下列函数中，既是奇函数，又是增函数是（ ）
A
B
C
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
12．已知定义在R上的奇函数
①对任意x，都有
②当
则
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
11．已知数列
A
B
C
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
17． 已知函数
（I）求函数
（II）设△ABC的内角A，B，C对边分别为a，b，c，且
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
19．在边长为a的正方形ABCD中，M，E，F，N分别为AB，BC，CD，CF的中点，现沿AE、AF、EF折叠，使B、C、D三点重合，构成一个三棱锥B - AEF，如图所示．
（I）在三棱锥B—AEF中，求证：AB⊥EF；
（II）求四棱锥E—AMNF的体积．
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
20．设椭圆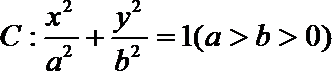
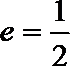
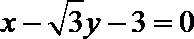
（I）求椭圆C的方程；
（II）在（I）的条件下，过右焦点F2作斜率为k的直线
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
18．第12届全国人民代表大会于2013年3月在北京召开，为了搞好对外宣传工作，会务组选聘了16名男记者和1 4名女记者担任对外翻译工作，调查发现，男、女记者中分别有10人和6人会俄语．
（I）根据以上数据完成以下2×2列联表：
并回答能否在犯错的概率不超过0.10的前提下认为性别与会俄语有关？
参考公式：
参考数据：
（II）会俄语的6名女记者中有4人曾在俄罗斯工作过，若从会俄语的6名女记者中随机抽取2人做同声翻译，则抽出的2人都在俄罗斯工作过的概率是多少？
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
21．设函数
（I）当a=1时，求函数
（II）当a≥2时，讨论函数
（III）若对任意a∈(2，3)及任意
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
请从22-24题中任选一题作答
22.如图，AB是圆O的直径，以B为圆心的圆B与圆O的一个交 点为P．过点A作直线交圆O于点Q，交圆B于点M，N．
（I）求证：QM=QN；
（II）设圆O的半径为2，圆B的半径为1．当AM=
23． 已知在平面直角坐标系xOy中，圆C的参数方程为
（I）写出直线l的直角坐标方程和圆C的普通方程；
（II）求圆C截直线l所得的弦长．
24． 设
（I）求不等式
（II）若关于x不等式
正确答案
22.
23.
24.
解析
解析已在路上飞奔，马上就到！
知识点
15．在三棱锥A—A′B′C′中，已知AA′⊥平面ABC，AA′=2，BC=
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
13.某乡镇供电所为了调查农村居民用电量情况，随机抽取了500户居民去年的用电量（单位：kw／h），将所得数据整理后，画出频率分布直方图如下；其中直方图从左到右前3个小矩形的面积之比为1：2：3。该乡镇月均用电量在37～39之内的居民共有____户．
正确答案
125
解析
解析已在路上飞奔，马上就到！
知识点
14．已知点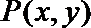
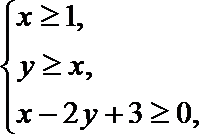
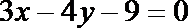
正确答案
2
解析
解析已在路上飞奔，马上就到！
知识点
16．给出以下四个结论：
①若实数
②若将函数
③曲线
④已知命题p：抛物线y= 2x2的准线方程为y= -
其中正确结论的序号是：_____________．（把所有正确结论的序号都填上）．
正确答案
（2）（3）（4）
解析
解析已在路上飞奔，马上就到！