- 真题试卷
- 模拟试卷
- 预测试卷
1．集合
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
4．已知函数f（x）＝
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
5．已知命题
A命题
B命题
C命题
D命题
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
7．设a＝0.50.5，b＝0．30.5，c＝log0.30.2，则a，b，c的大小关系是（ ）
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
10．定义在
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
2．函数
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
3．函数
A
B
C
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
6．已知α：x≥a，β：
A
B
C
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
9．已知定义在R上的函数y＝f（x）满足f（x＋2）＝f（x），当－1<x≤1时，f（x）＝x，若函数g（x）＝f（x）－loga|x|至少有5个零点，则a的取值范围是（ ）
A（1，5）
B（0，
C（0，
D[
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
8．已知函数f（x）＝x2＋mx＋ln x是单调递增函数，则m的取值范围是（ ）
Am>－2
Bm≥－2
Cm<2
Dm≤2
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
11．设复数z满足（1－i）z＝2i，则z＝ （ ） 。
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
13．设
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
12．计算
正确答案
-1
解析
解析已在路上飞奔，马上就到！
知识点
14．若函数y＝a2x＋2ax－1（a>1）在[－1，1]上的最大值是14，则a的值为________．
正确答案
3
解析
解析已在路上飞奔，马上就到！
知识点
15．设函数f（x）是定义在R上的偶函数，且对任意的x∈R恒有f（x＋1）＝f（x－1），已知当x1，x2∈[0，1]且x1<x2时，（x2－x1）[f（x1）－f（x2）]＞0，则有
①2是函数f（x）的周期；
②函数f（x）无最大值，有最小值是0；
③函数f（x）在（1，2）上是减函数，在（2，3）上是增函数；
④函数的对称轴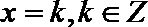
其中所有正确命题的序号是________．
正确答案
①④
解析
解析已在路上飞奔，马上就到！
知识点
16．一汽车厂生产A，B，C三类轿车，每类轿车均有舒适型和标准型两种型号，某月的产量如下表（单位：辆）：
按类用分层抽样的方法在这个月生产的轿车中抽取50辆，其中有A类轿车10辆．
（1）求z的值；
（2）用分层抽样的方法在C类轿车中抽取一个容量为5的样本．将该样本看成一个总体，从中任取2辆，求至少有1辆舒适型轿车的概率．
正确答案
（1）400
（2）
解析
解析已在路上飞奔，马上就到！
知识点
18．如图所示，在四棱锥PABCD中，AB⊥平面PAD，AB∥CD，PD＝AD，E是PB的中点，F是DC上的点且DF＝
（1）证明：PH⊥平面ABCD；
（2）若PH＝1，AD＝
正确答案
（1）证明：由于AB⊥平面PAD，
PH
又∵PH为△PAD中AD边上的高，
∴ AD⊥PH．
∵ AB∩AD＝A，AB
AD
∴ PH⊥平面ABCD．
（2）由于PH⊥平面ABCD，
E为PB的中点，PH＝1，
故E到平面ABCD的距离h＝
又∵ AB∥CD，AB⊥AD，∴ AD⊥CD，
故S△BCF＝
因此VEBCF
＝
＝
解析
解析已在路上飞奔，马上就到！
知识点
20．定义在D上的函数
（1）当
（2）若函数
正确答案
（1）
（2）
解析
解析已在路上飞奔，马上就到！
知识点
17．已知函数f（x）＝2sin x cos x－
（1）求f（x）的最小正周期；
（2）当x∈
正确答案
（1）T=
（2）最大3最小2
解析
解析已在路上飞奔，马上就到！
知识点
21．已知函数
（Ⅰ）若函数
（Ⅱ）设函数
（Ⅲ）设
正确答案
略
解析
解析已在路上飞奔，马上就到！
知识点
19．正项等比数列{an}中，
（1）求数列{an}的通项公式；
（2）若数列{bn}满足：
正确答案
（1）
（2）
解析
解析已在路上飞奔，马上就到！