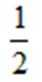- 真题试卷
- 模拟试卷
- 预测试卷
3．若
A
B
C
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
5．已知双曲线
A
B2
C1
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
6．已知关于x的不等式x2－4ax＋3a2<0(a>0)的解集为(x1，x2)，则x1＋x2＋
A
B
C
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
9．已知某程序框图如图所示，则该程序运行后输出的结果为（ ）
A
B
C
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
7．“
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
1．设集合
A
B
C
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
4．在
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
8．某几何体的三视图如下图所示，则其体积为（ ）
A
B
C
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
12．已知函数
A函数
B若函数
C函数
D函数
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
11．已知点
A
B
C
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
2．已知复数
A0
B
C
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
10．能够把圆
A
B
C
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
13．设x，y满足约束条件
正确答案
8
解析
解析已在路上飞奔，马上就到！
知识点
15．观察下列等式：
照此规律，第五个等式为__________。
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
14．tan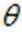
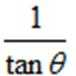
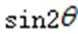
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
16．已知正方体
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
17．函数
（1）求函数
（2）在△
正确答案
解:
（1）
∵最高点与相邻对称中心的距离为
即
又
即
∴
（2）
∵
又
由余弦定理得
解析
解析已在路上飞奔，马上就到！
知识点
19．如图，菱形
（1）求证：
（2）求三棱锥
正确答案
解：
（1）证明：因为点
所以
所以
因为
所以
（2）三棱锥
由题意，
因为
又因为菱形
因为
所以
所求体积等于
解析
解析已在路上飞奔，马上就到！
知识点
21．已知函数
（1）求
（2）对函数
正确答案
解：
（1）由
而点
故有
（2）由（1）得
令
令
故当
当
当
故
要使
解析
解析已在路上飞奔，马上就到！
知识点
18．了响应政府“节能、降耗、减排、增效”的号召，某工厂决定转产节能灯，现有A，B两种型号节能灯的生产线供选择；从这两种生产线生产的大量节能灯中各随机抽取100个进行质量评估，经检验，综合得分情况如下面的频率分布直方图：
产品级别划分以及利润如下表：
视频率为概率．
（1）估计生产A型节能灯的一级品率．
（2）估计生产一个B型节能灯的利润大于0的概率，并估计生产品100个B型节能灯的平均利润。
正确答案
解：
解析
解析已在路上飞奔，马上就到！
知识点
20．已知圆
（1）求动圆圆心
（2）设斜率为
正确答案
解：
（1）圆
（2）设直线
所以
线段
将点
解析
解析已在路上飞奔，马上就到！
知识点
选做题：请考生在第22、23、24三题中任选一题做答，如果多做，则按所做的第一题记分．
22．选修4—1：几何证明选讲
如图，
（1）求证：
（2）求证：
23．选修4-4：坐标系与参数方程
已知平面直角坐标系
（1）写出曲线C的普通方程和极坐标方程；
（2）求|AB|的值。
24．选修4－5：不等式选讲
已知
（1）当
（2）如果函数
正确答案
22.
证明：
（1）连接
又
又
所以
所以
（2）延长
因为
所以
23.
解：
（1）曲线C的参数方程为：
消参数
由曲线C的普通方程为：
所以曲线C的极坐标方程为：
（2）由点A，B的极坐标分别为：
得点A，B的直角坐标分别为：
所以
24.
解：
（1）{x|x≥2或x≤-4}．
（2）（-2，2）
①当a=1时，f（x）=|2x-1|+x-5=
由
∴f（x）≥0的解为{x|x≥2或x≤-4}．
②由f（x）=0得|2x-1|=-ax+5．作出y=|2x-1|和y=-ax+5 的图象
观察可以知道，当-2＜a＜2时，这两个函数的图象有两个不同的交点，函数y=f（x）有两个不同的零点．故a的取值范围是（-2，2）．
解析
解析已在路上飞奔，马上就到！