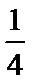- 真题试卷
- 模拟试卷
- 预测试卷
1.已知集合


正确答案
解析



考查方向
解题思路
先计算出A集合再求2个集合的交集。
易错点
粗心做错。
知识点
2.已知


正确答案
解析
由已知


考查方向
解题思路
将i乘到右边再利用复数相等分别求出a,b,代入即可解出。
易错点
计算失误。
知识点
3.中国古代数学著作《算法统宗》中有这样一个问题:“三百七十八里关,初行健步不为难,次日脚痛减一半,六朝才得到其关,要见次日行里数,请公仔细算相还。”其意思为:“有
正确答案
解析
由题意可知

考查方向
解题思路
由已知可得等比数列的公比是1/2,前六项的和为378,可以求出首项,进一步求出第二项即可。
易错点
不会转化为等比数列来做。
知识点
5.知函数

正确答案
解析
将2个函数利用诱导公式先进行化简,


考查方向
解题思路
逐一进行判断。
易错点
性质弄错。
知识点
6.已知抛物线

正确答案
解析
由题意可知抛物线的焦点坐标为


考查方向
解题思路
先根据抛物线找到焦点坐标从而求出双曲线中的未知数a,再进一步求出双曲线的离心率。
易错点
计算失误。
知识点
7.设曲线





正确答案
解析
先计算出g(x)并可知是偶函数,
考查方向
解题思路
先计算出g(x)并可知是偶函数,然后再来根据相乘之后去找到相应的函数的图像。
易错点
弄不清楚函数的奇偶性及图像的特征。
知识点
8.执行如图所示的程序框图,则输出的结果是( )
正确答案
解析
由判断框的条件来执行循环最后可以得到正确答案是B.
考查方向
解题思路
按步骤来计算。
易错点
计算出错。
知识点
4.已知



正确答案
解析
【解析】由“

考查方向
解题思路
直接根据定义来判断。
易错点
判断出错。
知识点
9.如图,在正四棱柱




正确答案
解析
由图像可知其正视图的面积是一个定值1,而俯视图显然面积最大为1/2,正视图与俯视图的面积之比的最小值为2,所以选B答案。
考查方向
解题思路
分别找到正视图和俯视图什么时候取到最值然后计算出来。
易错点
不知道什么时候比值最小。
知识点
10.已知



正确答案
解析
由函数



考查方向
解题思路
利用奇函数的定义最后转化过来求解。
易错点
不知道怎么转化为所学内容来做。
知识点
12.若函数


正确答案
解析
解答此题可以用特殊方法来做,将a=0代入可以满足题意,然后再代入a的值找出正确答案是B.
考查方向
解题思路
由于最大值是
易错点
没有分类讨论。
知识点
11.已知 







正确答案
解析
【解析】由








考查方向
解题思路
可以将其中一个向量的模设出来,其他 的用所设的表示出来,最后利用向量的数量积定义的变形式即可解出来。
易错点
不会利用数量积来求解。
知识点
13.一只蜜蜂在一个半径为3的球体内自由
正确答案
解析


考查方向
解题思路
本题考查几何概型,转化为体积之比即可算出。
易错点
不理解题意,不会转化为体积之比来做。
知识点
14.若
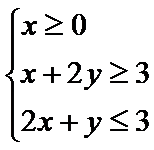

正确答案
解析
如图所示,

考查方向
解题思路
本题考查了简单的线性规划问题,先作出可行域,然后求出取值范围。
易错点
取值的时候弄错。
知识点
15.已知抛物线方程为











正确答案
解析
根据抛物线的定义到y轴的距离等于到焦点的距离减去1,所以m+1+n的最小值就等于焦点到直线的距离d,所以可以解得则

考查方向
解题思路
本题考查数形结合思想来解答,画出示意图,然后求出最值。
易错点
不会想到抛物线的定义来解答。
知识点
16.已知数列






正确答案
6
解析
由题意可知
=1,然后利用等差数列的前n项和公式即可解得k=6.
考查方向
解题思路
本题考查等差数列的前n项和的性质,利用性质构造一个方程组即可解出来。
知识点
17.在



(1)求角



正确答案
(1)
解析
试题分析:本题属简单的三角恒定变换和解三角形的问题,(1)先由正弦定理将边的关系转化为角的关系然后化简之后可以求出角B;(2)利用余弦定理以及已知条件即可解出三角形的面积。
试题解析:(1)∵

∴
∵

∵

∵


(2)将



即
∴

于是, 
考查方向
解题思路
本题考查了简单的三角恒定变换和解三角形的问题,解题步骤如下:(1)先由正弦定理将边的关系转化为角的关系然后化简之后可以求出角B;(2)利用余弦定理以及已知条件即可解出三角形的面积。
易错点
一般是容易出现计算失误。
知识点
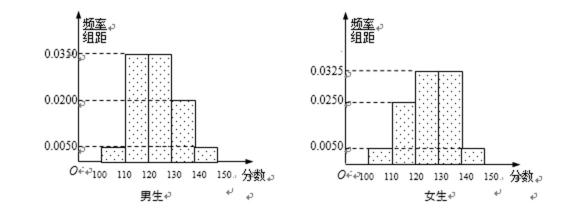
18.某学校高三年级有学生500人,其中男生300人,女生200人,为了研究学生的数学成绩是否与性别有关,现采用分层抽样的方法,从中抽取了100名学生,先统计了他们期中考试的数学分数,然后按性别分为男、女两组,再将两组学生的分数分成5组:[100,110),[110,120),[120,130),[130,140),[140,150]分别加以统计,得到如图所示的频率分布直方图.
(1)从样本中分数小于110分的学生中随机抽取2人,求两人恰好为一男一女的概率;
(2)若规定分数不小于130分的学生为“数学尖子生”,
附:
正确答案
(1)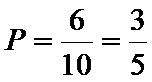
解析
试题分析:本题属古典概型及独立性检验,(1)先根据分层抽样算出抽出的人数,然后利用古典概型的公式计算;(2)列出联表然后代入公式计算出k的观测值,然后下结论。
试题解析:(1)解:由已知得,抽取的100名学生中,男生60名,女生40名
分数小于等于110分的学生中,
男生人有60×0.05 = 3(人),记为A1,A2,A3;女生有40×0.05 = 2
从中随机抽取2名学生,所有的可能结果共有10种,
(A2,A3),(A1,B1),(A1,B2),(A2,B1),(A2,B2),(A3,B1),(A3,B2),(B1,B2)
其中,两名学生恰好为一男一女的可能结果共有6种,它们是:(A1,B1),(A1,B2),
(A2,B1),(A2,B2),(A3,B1),(A3,B2),
故所求的概率
(2)解:由频率分布直方图可知,
在抽取的100名学生中,男生 60×0
据此可得2×2列联表如下:
所以得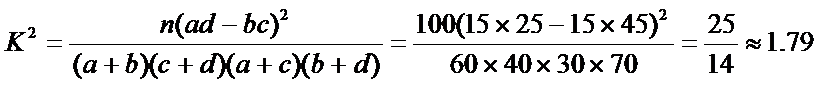
因为1.79 < 2.706.
所以没有90%的把握认为“数学尖子生与性别有关”.
考查方向
解题思路
本题考查了古典概型及独立性检验,解题步骤如下:(1)先根据分层抽样算出抽出的人数,然后利用古典概型的公式计算;(2)列出联表然后代入公式计算出k的观测值,然后下结论。
易错点
在找基本事件的个数的时候有可能遗漏或者重复。
知识点
20.如图,已知椭圆






(1)求圆C的半径
(2)若点


交直线


正确答案
(1)
解析
试题分析:本题属直线与圆锥曲线的位置关系的问题,题目的难度是逐渐由易到难,(1)直接按照步骤来求;(2)利用设而不求的方法再结合基本不等式来求解。
试题解析::(1)依题意得,
设点



∴点





当两圆外切时,圆心距
当两圆内切时,圆心距
∴


由




解得点

把直线





所以
(∵求最大值,显然
当且仅当
∴


考查方向
解题思路
本题考直线与圆锥曲线的位置关系,解题步骤如下:(1)直接按照步骤来求;(2)利用设而不求的方法再结合基本不等式来求解。
易错点
计算量大容易算错。
知识点
19. 如图,空间几何体








(1)试确定点


(2)在(1)的条件下,平面



正确答案
(1)M是线段AE的中点,证明见解析;(2)
解析
试题分析:本题属立体几何中的有关证明和体积有关的计算问题,题目的难度是逐渐由易到难,(1)根据线面平行的判定定理来证明;(2)将2个几何体的体积计算出来再计算出比值。
试题解析:(Ⅰ)当M是线段AE的中点时,AC//平面MDF,证明如下: 1
连结CE交DF于N,连结MN,由于M、N分别是AE、CE的中点,
所以MN//AC,又MN在平面MDF内, 所以AC//平面MDF (

三棱柱ADE-



又 三棱锥F-DEM的体积


考查方向
解题思路
本题考查了立体几何中的有关证明和体积有关的计算问题,解题步骤如下:(1)根据线面平行的判定定理来证明;(2)将2个几何体的体积计算出来再计算出比值。
易错点
不会求体积。
知识点
21.已知函数




(1)求实数
(2)当



正确答案
(1)
解析
试题分析:本题属于函数与导数的应用,题目的难度是逐渐由易到难,(1)求导之后得到a的一个范围,最后再得到关于a的一个不等式;(2)分类讨论求解。
试题解析:(1)0令
由题意:△

且
∵

∴
(2)又∵
∴


又∵
①当



∴当





∴当

∴
考查方向
解题思路
本题考查了函数与导数的应用,解题步骤如下:(1)求导之后得到a的一个范围,最后再得到关于a的一个不等式;(2)分类讨论求解。
易错点
不会转化为所学的内容来做。
知识点
22.如图所示,













(1)求证:
(2)求
正确答案
(1)见解析;(2)
解析
试题分析:本题属于几何证明选讲问题,(1)利用三角形相似来证明;(2)利用切割线定理然后利用三角形相似来解答。
试题解析:(Ⅰ)∵ 




∴
(2)∵





又由(Ⅰ)知
连接


∴
考查方向
解题思路
本题考几何证明选讲问题,解题步骤如下:(1)利用三角形相似来证明;(2)利用切割线定理然后利用三角形相似来解答。
易错点
不会转化。