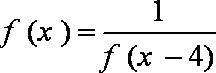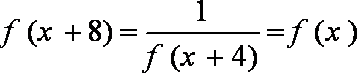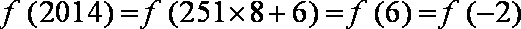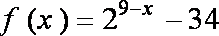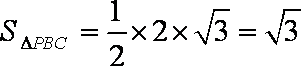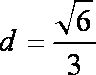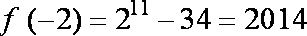- 真题试卷
- 模拟试卷
- 预测试卷
4.某几何体的三视图如下图所示,则该几何体的表面积为( )
正确答案
解析
由三视图可知几何体为下部是底面半径为3,高为6的圆柱,上部是侧棱长为5,底面边长为





知识点
7.已知


正确答案
解析
因为





所以



知识点
9.平面上画了一


正确答案
解析
由于平行线相距



知识点
1. 下列关于不等式的说法正确的是( )
正确答案
解析
根据基本不等式成立的条件是“一正二定三相等”可知A不正确,因为a、b不一定是正实数;C中一元二次方程的根是1+a和1-a,但是当



知识点
5.如下流程图所示的程序,如果输出i=3,则x的最小值为( )
正确答案
解析
运行流程图,由于输出i=3.所以i=1时,





知识点
6.已知x、y满足约束条件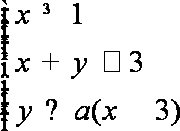
正确答案
解析
先画出可以确定的可行域,再根据含参数a的直线过定点(0,3),考虑该直线与直线x=1交于点
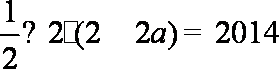
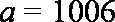
知识点
3.在
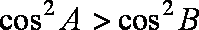
正确答案
解析
因为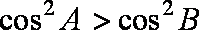

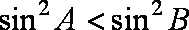
即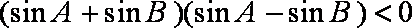
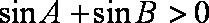
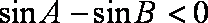
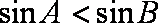
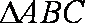
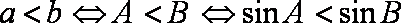
知识点
2.已知集合

正确答案
解析
因为


知识点
8.设函数



正确答案
解析
因为函数







知识点
10.抛物线

正确答案
解析
知识点
20.设函数
(Ⅰ)若曲线


(Ⅱ)讨论
(Ⅲ)讨论方程
正确答案
见解析。
解析
(Ⅰ)因为曲线




所以


所以当











在
(Ⅲ)因为方程

令


解得x=-1(舍),x=1,所以

所以
当b-1>0即b>1时,方程
当b=1时,方程
当b<0时,方程
知识点
19.正项数列

(Ⅰ)求出





正确答案
见解析。
解析
(Ⅰ) 
所以



(Ⅱ)因为


所以
知识点
16.已知A、B、C是



(Ⅰ)求角B的大小;
(Ⅱ)若

正确答案
见解析。
解析
(Ⅰ)∵向量


所以
由正弦定理可得:
再由余弦定理可得:
(Ⅱ)由(Ⅰ)得

所以

所以
知识点
17.北师大和华师大两所高校,准备从2014年毕业生中各选派1名优秀毕业生去汶川和玉树地区从事教育教学工作,其中北师大有2名男生1名女生报名,华师大有1名男生和2名女生报名.
(Ⅰ)若从两所学校报名的学生中各任选一名,写出所有可能的结果,并求选出的2名学生性别相同的概率;
(Ⅱ)若从报名的6名学生中任选2名,写出所有可能的结果,并求选出的2名教师来自同一学校的概率.
正确答案
见解析。
解析
记北师大的学生为





(Ⅰ)由题意知从两所学校报名的学生中各任选一名,写出所有可能的结果为(

















所以选出的2名学生性别相同的概率
(Ⅱ) 若从报名的6名学生中任选2名,写出所有可能的结果(





























所以选出的2名教师来自同一学校的概率为
知识点
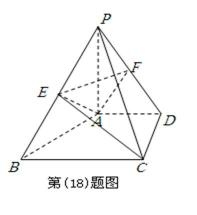
18.已知如图,四边形ABCD是直角梯形,AD//BC,CD⊥AD,PA⊥平面ABCD,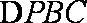
(Ⅰ)求证:BD//平面AEF;
(Ⅱ)求点A到平面PBC的距离.
正确答案
见解析。
解析
(Ⅰ)证明:连接BD,因为E、F分别是PB、PD的中点.在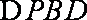

(Ⅱ)设A到平面PBC的距离为d,因为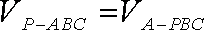
即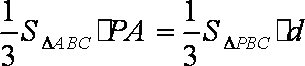
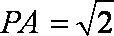
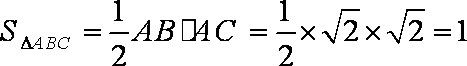
所以
知识点
21.已知如图,在平面直角坐标系xoy中,点B

(Ⅰ)求出椭圆C的方程;
(Ⅱ)当直线PA平分FB时,求k的值;
(Ⅲ)当k=2时,求点P到直线AC的距离;
(Ⅳ)是否存在正实数k使
正确答案
见解析。
解析
(Ⅰ)因为椭圆C的长轴长为4,点B



(Ⅱ)由题意可知F为


(Ⅲ)当k=2时,直线l的方程为

解得P点为




(Ⅳ)存在正实数k使

可得




所以
因为k(k>0),当且仅当


知识点
13.已知数列


正确答案
解析
因为

当n为奇数时,
当n为偶数时,
知识点
11.已知曲线

正确答案

解析
分焦点在x轴和y轴上两种情况,
当焦点在x轴上时,

当焦点在y轴上时,

知识点
12.已知




正确答案
解析
以共顶点,长度为1的两个线段为领边作平行四边形,考虑从此顶点出发的对角的长度,易得在夹角为



知识点
15.把正偶数依次按如下规律进行排序:第一个括号括一个数,第二个括号括两个数,第三个括号括三个数,第四个括号括一个数,…,依次循环,如(2),(4,6),(8,10,12),(14),…,则第50个括号内的各数的和为 .
正确答案
394
解析
由题意可知,每三个括号将用掉数列的6项,所以前49个括号共用了数列的97项,第50个括号里有两个数分别是196和198,故两个数的乘积为394.
知识点
14.14.若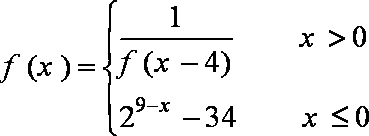

正确答案
2014
解析
x>0时,因为