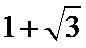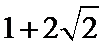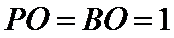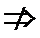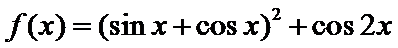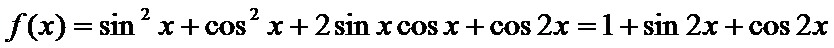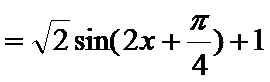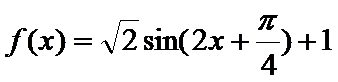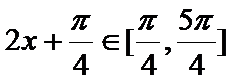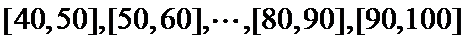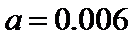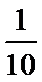- 真题试卷
- 模拟试卷
- 预测试卷
2.设全集



正确答案
解析
∵

考查方向
解题思路
先算出补集,然后求交集
易错点
求集合的交集和补集时错误
知识点
5.已知x,y满足约束条件

正确答案
解析
根据题意作出约束条件确定的可行域,如下图:
令


考查方向
解题思路
先根据约束条件画出可行域,然后用目标函数判断最值
易错点
画可行域时错误
知识点
7.执行如图所示的程序框图(算法流程图),输出的n为( )
正确答案
解析
执行第一次循环体:
执行第二次循环体:
执行第三次循环体:

考查方向
解题思路
根据题意执行多次循环体,然后判断循环停止的条件,进而得到输出结果
易错点
循环、顺序语序掌握不好,计算错误
知识点
8.直线3x+4y=b与圆
正确答案
解析
∵直线


考查方向
解题思路
先确定圆的圆形,然后用点到直线的距离公式求解
易错点
圆的一般方程转换成标准方程换错,点到直线的距离求错
知识点
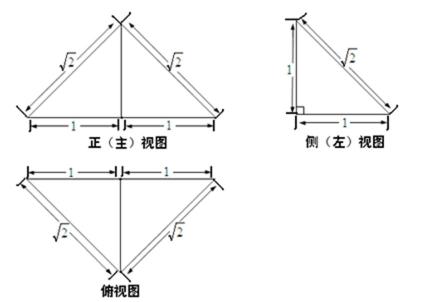
9.一个四面体的三视图如图所示,则该四面体的表面积是( )
正确答案
解析
由该几何体的三视图可知,该几何体的直观图,如下图所示:
其中侧面PAC⊥底面ABC,且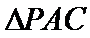
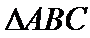
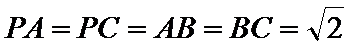
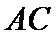
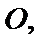
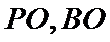
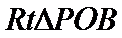
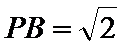
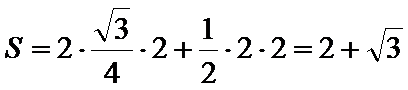
考查方向
解题思路
先根据三视图还原成直观图,然后根据立体几何相关性质求解。
易错点
立体感不强,三视图还原成直观图错误
知识点
1.设

正确答案
解析
因为
考查方向
解题思路
根据题意按照步骤化简
易错点
复数的概念理解不深,复数的计算出错
知识点
3.设p:x<3,q:-1
正确答案
解析
∵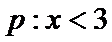
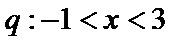
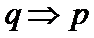
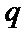
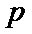
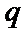
考查方向
解题思路
先根据题意,求出命题P和命题q,然后在进行判断
易错点
充分条件和必要条件记忆混淆
知识点
4.下列函数中,既是偶函数又存在零点的是( )
正确答案
解析
选项A:

选项B:

选项C:
选项D:
且

考查方向
解题思路
根据偶函数和零点的性质,结合选项,逐一判断。
易错点
对函数的零点的概念掌握不好,不会判断函数有无零点
知识点
6.下列双曲线中,渐近线方程为
正确答案
解析
由双曲线的渐进线的公式可行选项A的渐进线方程为
考查方向
解题思路
根据选项逐一判断
易错点
求渐近线方程错误,双曲线相关性质掌握不好
知识点
10.函数
正确答案
解析
由函数

又


由图可知
∴
考查方向
解题思路
先根据图像和函数相关性质、单调性、奇偶性、拐点等性质进行判断参数的符号。
易错点
数形结合思想掌握不好,函数相关性态求解有问题
知识点
13.已知数列




正确答案
27
解析
∵
∴

∴
考查方向
解题思路
根据题意先求判断数列是等差数列,然后求出等差数列的公差。
易错点
分类讨论思想,数列求和错误。
知识点
11.
正确答案
-1
解析
原式=
考查方向
解题思路
按照相关性质逐步计算求得
易错点
对数及指数幂的计算错误
知识点
14.在平面直角坐标系



正确答案
解析
在同一直角坐标系内,作出
由题意,可知
考查方向
解题思路
先根据题意作出函数的大致图象,然后根据图像判断
易错点
数形结合思想运用不好,不会想到作图
知识点
15.



①




正确答案
①④⑤
解析
∵等边三角形ABC的边长为2,



∵



∴
考查方向
解题思路
根据题意逐一判断序号。
易错点
平面向量的基本性质混淆,向量的数量积求解错误,计算能力弱
知识点
12.在




正确答案
2
解析
由正弦定理可知:
考查方向
解题思路
先根据正弦定理确定比例等量关系,然后求解AC长
易错点
想不到用正弦定理求解,计算能力弱
知识点
已知函数
16.求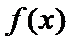
17.求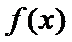
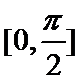
正确答案
(Ⅰ)
解析
(Ⅰ)因为
所以函数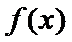
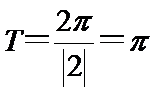
考查方向
解题思路
先化简,然后再求出三角函数的最小正周期
易错点
三角函数化简时错误
正确答案
(Ⅱ)最大值为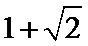
解析
(Ⅱ)由(Ⅰ)得计算结果,
当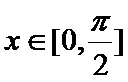
由正弦函数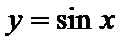
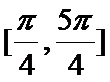
当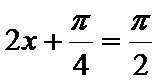
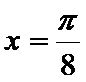
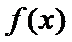
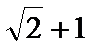
当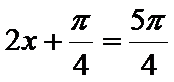
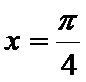
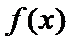

综上,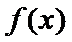
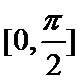

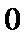
考查方向
解题思路
根据第一问结果,结合函数图象判断求解
易错点
根据第一问求出的一般形式判断函数最值
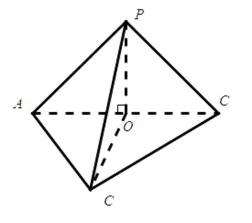
如图,三棱锥P-ABC中,PA

23.求三棱锥P-ABC的体积;
24.证明:在线段PC上存在点M,使得AC

正确答案
(Ⅰ)
解析
(Ⅰ)解:由题设

可得
由
可知

所以三棱锥
考查方向
解题思路
先找三棱锥的高,然后再求体积
易错点
找不到关键的线段,或者找到线段求不出来线段的长
正确答案
(Ⅱ)
解析
(Ⅱ)证:在平面







由









在直角




考查方向
解题思路
先求NC的长,然后利用比例的性质,求
易错点
辅助线的作法,解直角三角形时求解错误,计算能力弱
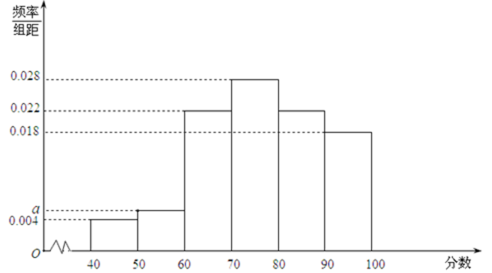
某企业为了解下属某部门对本企业职工的服务情况,随机访问50名职工,根据这50名职工对该部门的评分,绘制频率分布直方图(如图所示),其中样本数据分组区间为
18.求频率分布图中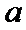
19.估计该企业的职工对该部门评分不低于80的概率;
20.从评分在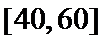
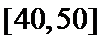
正确答案
(Ⅰ)0.006
解析
(Ⅰ)因为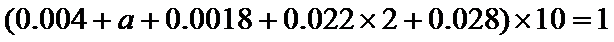
考查方向
解题思路
根据所给统计量计算求得
易错点
计算错误,对相关概念理解错误
正确答案
(Ⅱ)
解析
(Ⅱ)由所给频率分布直方图知,50名受访职工评分不低于80的频率为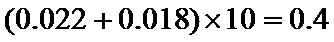
所以该企业职工对该部门评分不低于80的概率的估计值为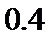
解题思路
根据频率分布直方图求得
易错点
频率求错,读图能力提信息时马虎大意。
正确答案
(Ⅲ)
解析
(Ⅲ)受访职工评分在[50,60)的有:50×0.006×10=3(人),即为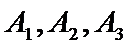
受访职工评分在[40,50)的有: 50×0.004×40=2(人),即为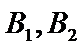
从这5名受访职工中随机抽取2人,所有可能的结果共有10种,它们是
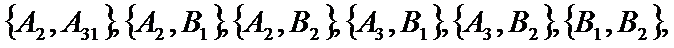
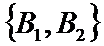
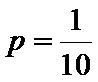
考查方向
解题思路
根据题意,按区间分别求概率
易错点
分类时错误,区间求概率时错误
已知数列
21.求数列
22.设




正确答案
(Ⅰ)
解析
(Ⅰ)由题设可知
又


由


考查方向
解题思路
先根据特殊项的值和关系,然后解出首项和公比
易错点
求数列通项公式时,不会利用数列的性质简便求解
正确答案
(Ⅱ)
解析
(Ⅱ)
又
所以

考查方向
解题思路
根据前n项和公式,整理得到裂项相消法得到新数列的和
易错点
求和时的方法选错或不会用裂项相消法求和
设椭圆E的方程为



25.求E的离心率e;
26.设点C的坐标为(0,-b),N为线段AC的中点,证明:MN
正确答案
(Ⅰ)
解析
(Ⅰ)解:由题设条件知,点


进而

证:由




又
由(Ⅰ)得计算结果可知


考查方向
解题思路
由题设条件,可得点





易错点
计算能力弱,圆锥曲线相关知识掌握不牢固,不系统
正确答案
详见解析.
解析
(Ⅱ)证:由




又
由(Ⅰ)得计算结果可知


考查方向
解题思路
利用向量的坐标表示求解,得到坐标数量积为0,进而得到线段垂直。
易错点
圆锥曲线的相关性质、概念、公式记忆错误,计算能力弱
已知函数
27.求

28.若


正确答案
(Ⅰ)递增区间是(-r,r);递减区间为(-∞,-r)和(r,+∞)
解析
(Ⅰ)由题意可知


所以当



因此,



考查方向
解题思路
对函数求导,结合函数定义域分段讨论函数的单调性
易错点
函数求导错误,分类讨论能力弱,计算能力弱
正确答案
(Ⅱ)极大值为100;无极小值.
解析
(Ⅱ)由(Ⅰ)的解答可知



因此





综上,
考查方向
解题思路
先根据第一问得到的答案,结合图像判断,极值是否存在。
易错点
函数求导错误,分类讨论能力弱,计算能力弱