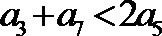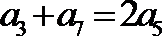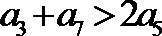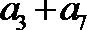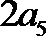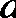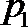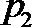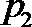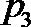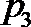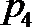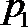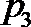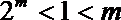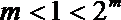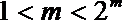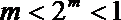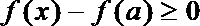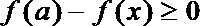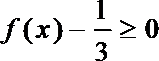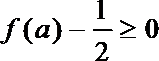- 真题试卷
- 模拟试卷
- 预测试卷
3．若偶函数
A
B
C
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
1．已知集合
A
B
C
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
4．函数
A
B
C
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
5．设
A
B
C
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
9．函数
A
B
C
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
2． 设
A
B
C
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
6．设点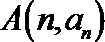
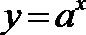
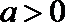
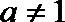
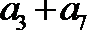
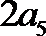
A
B
C
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
7．下面给出四个命题：
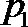
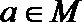
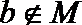
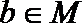
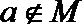
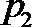
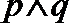
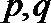
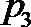
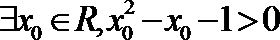
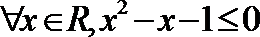
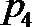
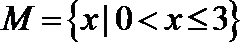
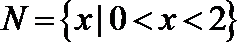
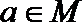
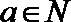
其中为真命题的是（ ）
A
B
C
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
8．设实数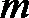
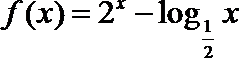
A
B
C
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
10．已知函数
A
B
C
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
12．定义在
A
B
C
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
11．已知函数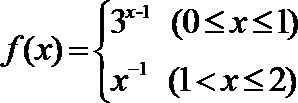
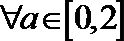
A
B
C
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
16．下面给出四个命题：
①函数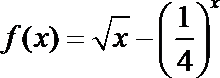
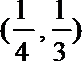
②若函数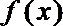
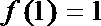
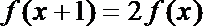
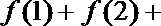
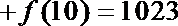
③“若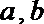
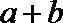
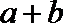
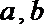
④“若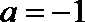
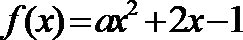
其中所有正确的命题序号是（ ）．
正确答案
②③
解析
解析已在路上飞奔，马上就到！
知识点
13．已知幂函数
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
14．设
正确答案
- 5
解析
解析已在路上飞奔，马上就到！
知识点
15．已知命题
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
19．已知函数f(x)＝(x＋2)|x－2|．
（1）若不等式f(x)≤a在[－3,1]上恒成立，求实数a的取值范围；
（2）解不等式f(x)>3x．
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
17．设函数f(x)＝log2(ax－bx) 且f(1)＝1，f(2)＝log212．
（1）求a、b的值；
（2）当x∈[1,2]时，求f(x)的最大值．
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
18．已知函数f(x)＝x＋
（1）f(x)的值域；
（2）若g(x)＝f(x)·x＋ax，且g(x)在区间（0,1）及（1,2）上分别存在一个零点，求实数a的取值范围．
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
20．某服装厂生产一种服装，每件服装的成本为40元，出厂单价定为60元，该厂为鼓励销售商订购，决定当一次订购量超过100件时，每多订购一件，订购的全部服装的出场单价就降低0．02元，根据市场调查，销售商一次订购量不会超过600件．
（1）设一次订购x件，服装的实际出厂单价为p元，写出函数p＝f(x)的表达式；
（2）当销售商一次订购多少件服装时，该厂获得的利润最大？其最大利润是多少？
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
选做题（从下列三道解答题中任选一道作答，若多做，则按首做题计入总分）
22．选修4—1：几何证明选讲
如图，
（1）求证：
（2）求证：
23．选修4—4：坐标系与参数方程
在直角坐标系xoy中，以原点o为极点，以x轴正半轴为极轴，与直角坐标系xoy取相同的长度单位，建立极坐标系，设曲线C参数方程为
（1）写出曲线C的普通方程和直线
（2）求曲线C上的点到直线
24．选修4—5：不等式选讲
（1）已知x、y都是正实数，求证：
（2）设不等的两个正数a、b满足
22．选修4—1：几何证明选讲
如图，
（1）求证：
（2）求证：
23．选修4—4：坐标系与参数方程
在直角坐标系
（1）写出曲线C的普通方程和直线
（2）求曲线C上的点到直线
24．（本题满分10分）选修4—5：不等式选讲
（1）已知
（2）设不等的两个正数
正确答案
正确答案
正确答案
21．设函数
（1）求区间
（2）给定常数
正确答案
解析
解析已在路上飞奔，马上就到！